4 从观测序列中学习模型参数

4.1 最大期望对数似然

设有$K$条观测序列$ ^{[5]} $:

$$ X=\{O^k\}_{k=1}^K $$

模型参数$ ^{[5]} $:

$$ \lambda = (A,B,\Pi) $$

调整模型参数使得观测序列概率最大化，即可完成参数学习过程$ ^{[1]} $.

- 阅读剩余部分 -

3 查找最大概率状态序列

当给定模型参数$\lambda$和状态序列$O$时

3.1 Viterbi

目标为:

$$ \bar{Q} = \underset{Q}{\arg \max} P(Q, O | \lambda) $$

• 定义$ ^{[2]} $

$$ \begin{align} \delta_t(i) &= \underset{q_1,q_2,\cdots,q_{t-1}}{\max} P(q_1,q_2,\cdots,q_t=i, O_1, O_2, \cdots, O_t | \lambda) \\ \delta_{t+1}(j) &= \underset{i}{\max} [\delta_t(i) a_{ij}] b_j(O_{t+1}) \end{align} $$

每次选择过去的概率乘转换概率后的最大概率作为最佳概率, 只要保持跟踪记录上次选择的最大概率对应状态$ S_i $. 则得到了最大概率状态序列.

- 阅读剩余部分 -

2 向前向后算法(forward-backward)

给定模型参数，计算给定任意观测序列$ O $的概率$ ^{[2]} $.

$$ P(O|\lambda) = \sum_Q P(O, Q | \lambda) $$

$ Q $有$ N^T $种可能，很显然，计算复杂度$ o(N^T) $太高. 因此使用(forward-backward)向前向后算法实现可接受的计算复杂度.

- 阅读剩余部分 -

1 简介

HMM是Hidden Markov Models缩写, 1960s, Baum和他的同事发布一系列论文，1970s CMU的Baker用于实现语音处理,1970s IBM Jelinek和他的同事用于语音处理$^{[1]}$.

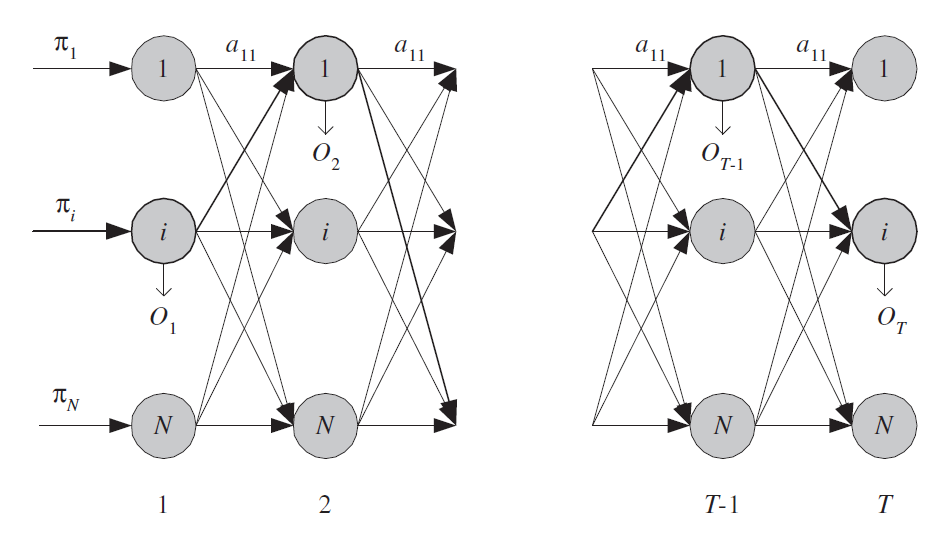
重要假设：当前状态仅与上一步状态相关，与上一步之前的状态无关.

- 阅读剩余部分 -