5. 连续观测

有两个方法将连续观测序列和HMM结合.

• 将连续观测聚类为离散类别,这就对应到HMM离散观测序列. 然后按照HMM离散观测序列处理.

• 更改观测概率函数为密度函数,例如高斯概率密度, 这需要替换观测状态序列生成函数.

5.1 替换观测概率为高斯密度

在离散观测序列中,发射函数\( b_j(m) \)定义为:

\[ B = [b_j(m)] \quad where \quad b_j(m) \equiv P(O_t = v_m | q_t = S_j) \]

将其替换为高斯密度函数(也可以是其他分布概率密度函数, 但参数更新部分需要同步替换),可以让HMM实现连续观测.

\[\begin{align}
B = [b_j(O_t)] & \equiv P(O_t | q_t = S_j, \lambda) \sim \mathcal{N}(\mu_j, \sigma_j^2) \\
&= \frac{1}{\sqrt{2 \pi \sigma_j^2}} \exp \left[ \frac{-(O_t – \mu_j)^2}{2 \sigma_j^2} \right]
\end{align}\]

参数更新:

\[\begin{align}
\bar{\mu}_j &= \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \gamma_t^k(i) O_t^k }{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \gamma_t^k(i)} \\
\bar{\sigma}_j^2 &= \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \gamma_t^k(i) (O_t^k – \bar{\mu}_j)^2 }{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \gamma_t^k(i)}
\end{align}\]

5.2 高斯混合分布

考虑观测序列为\( L \)个高斯分布按某比例混合.

\[\begin{align}
B = [b_j(O_t)] & \equiv P(O_t | q_t = S_j, \lambda) = \sum_{l=1}^L C_{jl} \mathcal{N}(O_t, \mu_{jl}, \sigma_{jl}^2) \\
\text{s.t.} \\
& \sum_{l=1}^L C_{jl} = 1.0
\end{align}\]

参数更新需要考虑混合系数,通过混合密度期望比例更新.

\[\begin{align}
\gamma_t^k(j, l) &= \gamma_t^k(j) \frac{C_{jl} \mathcal{N}(O_t^k, \mu_{jl}, \sigma_{jl}^2)}{\sum_{l=1}^L C_{jl} \mathcal{N}(O_t^k, \mu_{jl}, \sigma_{jl}^2)} \\
\bar{C}_{jl} &= \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \gamma_t^k(j,l)}{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \sum_{l=1}^L \gamma_t^k(j, l)} \\
\bar{\mu}_{jl} &= \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \gamma_t^k(j,l) O_t^k }{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \gamma_t^k(j,l)} \\
\bar{\sigma}_{jl}^2 &= \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \gamma_t^k(j,l) (O_t^k – \bar{\mu}_{jl})^2 }{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \gamma_t^k(j,l)}
\end{align}\]

5.3 多维高斯混合分布

多维相对单维只是替换了高斯函数,其余没有变化, \( d \)表示维度.

\[\begin{align}
\mathcal{N}(x, \mu, \Sigma) &= \frac{1}{ (2 \pi)^{\frac{d}{2}} |\Sigma|^{\frac{1}{2}} } \exp \left[ -\frac{1}{2} (x – \mu)^T \Sigma^{-1} (x – \mu) \right] \\
\gamma_t^k(j, l) &= \gamma_t^k(j) \frac{C_{jl} \mathcal{N}(O_t^k, \mu_{jl}, \Sigma_{jl})}{\sum_{l=1}^L C_{jl} \mathcal{N}(O_t^k, \mu_{jl}, \Sigma_{jl})} \\
\bar{\Sigma}_{jl} &= \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \gamma_t^k(j,l) (O_t^k – \bar{\mu}_{jl}) (O_t^k – \bar{\mu}_{jl})^T }{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \gamma_t^k(j,l)}
\end{align}\]

在多维分布计算中,连续观测序列的数据样本过少,样本各维度之间存在线形组合,会造成协方差矩阵奇异(共线/共面), 然后高斯函数计算失败. 因此样本数量需要远多于维度,且通过预处理消除线形组合维,如必要,可以有意添加噪声.

5.4 数值稳定

工程中使用\( \hat{\gamma}_t^k(j) \) 替换 \( \gamma_t^k(j) \), 否则可能因为序列过长导致计算结果超出机器精度容许范围.

5.5 代码试验

import numpy as np
from matplotlib import pyplot as plt

# multivaiance normal probability density function
def Multivar_Norm_PDF(x, mean, cov):
    dev = x - mean
    y = np.dot(dev, np.linalg.pinv(cov))  
    y = np.sum(y * dev, axis=0)  
    y = np.exp(  -0.5 * y )    
    y = (1.0 / ((2*np.pi)**(len(x) / 2) * np.linalg.det(cov) ** 0.5)) * y
    return y

# Gaussian mixture model
def GMM_PDF(x, coef, mean, cov):
    from scipy import stats
    v1 = sum([coef[l] * stats.multivariate_normal(mean[l], cov[l], True).pdf(x) for l in range(len(coef))])
    # v2 = sum([coef[l] * Multivar_Norm_PDF(x, mean[l], cov[l]) for l in range(len(coef))])
    # np.testing.assert_allclose(v1, v2, equal_nan=False, err_msg='cov compare')
    return v1

# the probability density of the model given observation sequence and state sequence
def PDFOQ(Q, O, Lambda):
  ''' p(Q,O | \lambda)=\prod^T_{t=1}p(q_t|q_{t-1}, \lambda)p(O_t|q_t, \lambda) '''
  A, B_coef, B_mean, B_cov, Pi = Lambda
  T = O.shape[0]
  assert( len(Q) == len(O) )
  assert( A.shape[0] == A.shape[1] == B_coef.shape[0] == Pi.shape[0] )
  assert( Q.min() >= 0 and Q.max() <  A.shape[0] )
  return np.prod([(A[Q[t-1], Q[t]] if t>0 else Pi[Q[t]]) * GMM_PDF(O[t], B_coef[Q[t]],B_mean[Q[t]],B_cov[Q[t]]) for t in range(T)])
 
# the log probability density of the model given observation sequence and state sequence
def logPDFOQ(Q, O, Lambda):
  ''' \log P(Q,O | \lambda)=\sum^T_{t=1} \log p(q_t|q_{t-1}, \lambda) + \log p(O_t|q_t, \lambda) '''
  A, B_coef, B_mean, B_cov, Pi = Lambda
  T = O.shape[0]
  assert( len(Q) == len(O) )
  assert( A.shape[0] == A.shape[1] == B_coef.shape[0] == Pi.shape[0] )
  assert( Q.min() >= 0 and Q.max() <  A.shape[0] )
  logPi, logA = np.log(Pi), np.log(A)
  return np.sum([(logA[Q[t-1], Q[t]] if t>0 else logPi[Q[t]]) + np.log(GMM_PDF(O[t], B_coef[Q[t]],B_mean[Q[t]],B_cov[Q[t]])) for t in range(T)])

# normal forward algorithm
class Alpha_GMM:
  def __init__(self, O, Lambda):
    self.O = O
    self.A, self.B_coef, self.B_mean, self.B_cov, self.Pi = Lambda
    self.T = len(O)
    self.N = self.A.shape[0]
    assert( self.A.shape[0] == self.A.shape[1] == self.B_coef.shape[0] == self.B_mean.shape[0] == self.Pi.shape[0] )
    assert( self.B_coef.shape[1] == self.B_mean.shape[1] == self.B_cov.shape[1] )
    assert( self.B_mean.shape[2] == self.B_cov.shape[2] == self.B_cov.shape[3] == len(self.O[0]) )
    '''
    \alpha_t(i) \equiv P(O_1 \cdots O_t, q_t = S_i | \lambda)
    notice: param t: 0=>t1, 1=>t2, ..., T-1=>T
    '''
    self.alpha = np.zeros(shape=(self.T, self.N))
    for t in range(self.T):
      if t == 0:
        self.alpha[t] = [self.Pi[i] * GMM_PDF(self.O[t], self.B_coef[i], self.B_mean[i], self.B_cov[i]) for i in range(self.N)]
      else:
        self.alpha[t] = [sum([self.alpha[t-1, h] * self.A[h, i] for h in range(self.N)]) * GMM_PDF(self.O[t], self.B_coef[i],self.B_mean[i],self.B_cov[i]) for i in range(self.N)]
 
  def __call__(self, t, i):
    return self.alpha[t, i]

# normal backword algorithm
class Beta_GMM:
  def __init__(self, O, Lambda):
    self.O = O
    self.A, self.B_coef, self.B_mean, self.B_cov, self.Pi = Lambda
    self.T = len(O)
    self.N = self.A.shape[0]
    assert( self.A.shape[0] == self.A.shape[1] == self.B_coef.shape[0] == self.B_mean.shape[0] == self.Pi.shape[0] )
    assert( self.B_coef.shape[1] == self.B_mean.shape[1] == self.B_cov.shape[1] )
    assert( self.B_mean.shape[2] == self.B_cov.shape[2] == self.B_cov.shape[3] == len(self.O[0]) )
    '''
    \beta_t(i) \equiv P(O_{t+1} \cdots O_T | q_t = S_i, \lambda)
    notice: param t: T=>T,T-1=>T-1,...,1=>t1,0=>t0
    '''
    self.beta = np.ones(shape=(self.T+1, self.N))
    for t in range(self.T-1, -1, -1):
      if t == 0:
        self.beta[t] = np.array([ self.Pi[j] * GMM_PDF(self.O[t], self.B_coef[j],self.B_mean[j],self.B_cov[j]) * self.beta[t+1, j] for j in range(self.N)]).sum()
      else:
        self.beta[t] = np.array([ self.A[:,j] * GMM_PDF(self.O[t], self.B_coef[j],self.B_mean[j],self.B_cov[j]) * self.beta[t+1, j] for j in range(self.N)]).sum(axis=0)
 
  def __call__(self, t, i):
    return self.beta[t, i]

# scaling forward algorithm
class Alpha_Hat_GMM:
  def __init__(self, O, Lambda):
    self.O = O
    self.A, self.B_coef, self.B_mean, self.B_cov, self.Pi = Lambda
    self.T = len(O)
    self.N = self.A.shape[0]
    assert( self.A.shape[0] == self.A.shape[1] == self.B_coef.shape[0] == self.B_mean.shape[0] == self.Pi.shape[0] )
    assert( self.B_coef.shape[1] == self.B_mean.shape[1] == self.B_cov.shape[1] )
    assert( self.B_mean.shape[2] == self.B_cov.shape[2] == self.B_cov.shape[3] == len(self.O[0]) )
    '''
    \hat{\alpha}_t(i) & \equiv P(q_t = S_i | O_1 \cdots O_t, \lambda)
    notice: param t: 0=>t1, 1=>t2, ..., T-1=>T
    '''
    self.C = np.zeros(shape=(self.T,))
    self.alpha_hat = np.zeros(shape=(self.T, self.N))
    for t in range(self.T):
      if t==0:
        self.alpha_hat[t] = [self.Pi[i] * GMM_PDF(self.O[t], self.B_coef[i],self.B_mean[i],self.B_cov[i]) for i in range(self.N)]
      else:
        self.alpha_hat[t] = [sum([self.alpha_hat[t-1, h] * self.A[h, i] for h in range(self.N)]) * GMM_PDF(self.O[t], self.B_coef[i],self.B_mean[i],self.B_cov[i]) for i in range(self.N)]
      self.C[t] = self.alpha_hat[t].sum()
      self.alpha_hat[t] /= self.C[t]
 
  def __call__(self, t, i):
    return self.alpha_hat[t,i]

# scaling backward algorithm
class Beta_Hat_GMM:
  def __init__(self, O, Lambda, C):
    self.O = O
    self.A, self.B_coef, self.B_mean, self.B_cov, self.Pi = Lambda
    self.T = len(O)
    self.N = self.A.shape[0]
    self.C = C
    assert( len(self.O) == len(self.C) )
    assert( self.A.shape[0] == self.A.shape[1] == self.B_coef.shape[0] == self.B_mean.shape[0] == self.Pi.shape[0] )
    assert( self.B_coef.shape[1] == self.B_mean.shape[1] == self.B_cov.shape[1] )
    assert( self.B_mean.shape[2] == self.B_cov.shape[2] == self.B_cov.shape[3] == len(self.O[0]) )
    '''
    \hat{\beta}_t(i) = \frac{ \beta_t(i) }{ \prod_{u=t+1}^T C_u } 
    notice: param t: T=>T,T-1=>T-1,...,1=>t1,0=>t0
    '''
    self.beta_hat = np.ones(shape=(self.T+1, self.N))
    for t in range(self.T-1, -1, -1):
      if t == 0:
        self.beta_hat[t] = np.array([ self.Pi[j] * GMM_PDF(self.O[t], self.B_coef[j],self.B_mean[j],self.B_cov[j]) * self.beta_hat[t+1, j] for j in range(self.N)]).sum()
      else:
        self.beta_hat[t] = np.array([ self.A[:,j] * GMM_PDF(self.O[t], self.B_coef[j],self.B_mean[j],self.B_cov[j]) * self.beta_hat[t+1, j] for j in range(self.N)]).sum(axis=0)
      self.beta_hat[t] /= self.C[t]
      
  def __call__(self, t, i):
    return self.beta_hat[t,i]

def Xi_GMM(t, i, j, O, Lambda, alpha, beta):
  # \xi_t(i, j) = \frac{ \alpha_t(i) a_{ij} b_j(O_{t+1}) \beta_{t+1}(j) }{ \sum_k^N \sum_l^N \alpha_t(k) a_{kl} b_l(O_{t+1}) \beta_{t+1}(l) }
  A, B_coef, B_mean, B_cov, Pi = Lambda
  N = Pi.shape[0]
  numerator = alpha(t, i) * A[i, j] * GMM_PDF(O[t+1], B_coef[j],B_mean[j],B_cov[j]) * beta(t+2, j)
  denominator = sum( [alpha(t, i) * A[i, j] * GMM_PDF(O[t+1], B_coef[j],B_mean[j],B_cov[j]) * beta(t+2, j) for i in range(N) for j in range(N)] )
  return numerator/denominator
 
def Xi_Hat_GMM(t, i, j, O, Lambda, alpha_hat, beta_hat):
  # \hat{\xi}_t(i, j) &= \frac{1}{C_{t+1}} \hat{\alpha}_t(i) a_{ij} b_j(O_{t+1}) \hat{\beta}_{t+1}(j)
  A, B_coef, B_mean, B_cov, Pi = Lambda
  numerator = alpha_hat(t, i) * A[i, j] * GMM_PDF(O[t+1], B_coef[j],B_mean[j],B_cov[j]) * beta_hat(t+2, j)
  denominator = alpha_hat.C[t+1]
  return numerator/denominator

def Gamma_GMM(t, i, O, Lambda, alpha, beta):
  # \gamma_t(i) = \frac{ \alpha_t(i) \beta_t(i) }{ \sum_l^N \alpha_t(l) \beta_t(l) }
  A, B_coef, B_mean, B_cov, Pi = Lambda
  N, L = B_coef.shape
  numerator = alpha(t, i) * beta(t+1, i)
  denominator = sum( [alpha(t, i) * beta(t+1, i) for i in range(N)] )
  return numerator / denominator

def Gamma_Hat_GMM(t, i, O, Lambda, alpha_hat, beta_hat):
  # \hat{\gamma}_t(i) &= \hat{\alpha}_t(i) \hat{\beta}_t(i)
  return alpha_hat(t, i) * beta_hat(t+1, i)

def Gamma_L_GMM(t, i, l, O, Lambda, alpha, beta):
    A, B_coef, B_mean, B_cov, Pi = Lambda
    num = B_coef[i,l] * GMM_PDF(O[t], [1.0], [B_mean[i,l]], [B_cov[i,l]])
    den = GMM_PDF(O[t], B_coef[i], B_mean[i], B_cov[i])
    p1 = Gamma_GMM(t, i, O, Lambda, alpha, beta)
    p2 = num / den
    return p1 * p2

def Gamma_Hat_L_GMM(t, i, l, O, Lambda, alpha_hat, beta_hat):
    A, B_coef, B_mean, B_cov, Pi = Lambda
    num = B_coef[i,l] * GMM_PDF(O[t], [1.0], [B_mean[i,l]], [B_cov[i,l]])
    den = GMM_PDF(O[t], B_coef[i], B_mean[i], B_cov[i])
    p1 = Gamma_Hat_GMM(t, i, O, Lambda, alpha_hat, beta_hat)
    p2 = num / den
    return p1 * p2

# find best state sequnce in the model given the parameters of the model and observation sequence
def Viterbi(O, Lambda):
  A, B_coef, B_mean, B_cov, Pi = Lambda
  T = O.shape[0]
  N = A.shape[0]
  assert( A.shape[0] == A.shape[1] == B_coef.shape[0] == B_mean.shape[0] == Pi.shape[0] )
  assert( B_coef.shape[1] == B_mean.shape[1] == B_cov.shape[1] )
  assert( B_mean.shape[2] == B_cov.shape[2] == B_cov.shape[3] == len(O[0]) )
  
  delta = np.zeros(shape=(T, N))
  psi = np.zeros(shape=(T, N), dtype=np.int)
  for t in range(T):
    ''' 0=>t1, 1=>t2, ...,T-1=>T '''
    if t == 0:
      # \delta_1(i) &= \pi_i b_i(O_1)
      # delta[t] = Pi * B[:, O[t]]
      for i in range(N):
          delta[t,i] = Pi[i] * GMM_PDF(O[t], B_coef[i],B_mean[i],B_cov[i])
      # \psi_1(i) &= null
      psi[t] = np.nan
    else:
      # \delta_t(j) &= \underset{i}{\max} [\delta_{t-1}(i) a_{ij}] b_j(O_t)
      # \psi_t(j) &= \underset{i}{\arg \max} [\delta_{t-1}(i) a_{ij}] 
      for j in range(N):
        max_delta = max([(delta[t-1, i] * A[i, j] * GMM_PDF(O[t], B_coef[j],B_mean[j],B_cov[j]), i) for i in range(N)], key=lambda x:x[0])
        delta[t, j] = max_delta[0]
        psi[t, j] = max_delta[1]
        
  Q = np.zeros(shape=T, dtype=np.int)
  # \bar{P} &= \underset{i}{\max} \delta_T(i) 
  # \bar{q}_T &= \underset{i}{\arg \max} \delta_T(i) 
  P = np.max(delta[T-1])
  Q[T-1] = np.argmax(delta[T-1])
  # \bar{q}_t = \psi_{t+1}( \bar{q}_{t+1} ) \qquad \text{where} \qquad t=T-1,T-2,\cdots,2,1
  for t in range(T-2, -1, -1):
    Q[t] = psi[t+1, Q[t+1]]
    
  return Q, P

# find best state sequnce using log in the model given the parameters of the model and observation sequence
def logViterbi(O, Lambda):
  logA, B_coef, B_mean, B_cov, logPi = np.log(Lambda[0]), Lambda[1], Lambda[2], Lambda[3], np.log(Lambda[4])
  T = O.shape[0]
  N = logA.shape[0]
  assert( logA.shape[0] == logA.shape[1] == B_coef.shape[0] == B_mean.shape[0] == logPi.shape[0] )
  assert( B_coef.shape[1] == B_mean.shape[1] == B_cov.shape[1] )
  assert( B_mean.shape[2] == B_cov.shape[2] == B_cov.shape[3] == len(O[0]) )
  
  logdelta = np.zeros(shape=(T, N))
  logpsi = np.zeros(shape=(T, N), dtype=np.int)
  for t in range(T):
    ''' 0=>t1, 1=>t2, ...,T-1=>T '''
    if t == 0:
      # \delta_1(i) &= \pi_i b_i(O_1)
      # logdelta[t] = logPi + logB[:, O[t]]
      for i in range(N):
         logdelta[t,i] = logPi[i] + np.log(GMM_PDF(O[t], B_coef[i],B_mean[i],B_cov[i]))
      # \psi_1(i) &= null
      logpsi[t] = np.nan
    else:
      # \delta_{t+1}(j) = \underset{i}{\max} \delta_t(i) + \log a_{ij} + \log b_j(O_{t+1})
      # \psi_t(j) &= \underset{i}{\arg \max} [\delta_{t-1}(i) a_{ij}]
      for j in range(N):
        max_logdelta = max([(logdelta[t-1, i] + logA[i, j] + np.log(GMM_PDF(O[t], B_coef[j],B_mean[j],B_cov[j])), i) for i in range(N)], key=lambda x:x[0])
        logdelta[t, j] = max_logdelta[0]
        logpsi[t, j] = max_logdelta[1]
        
  logQ = np.zeros(shape=T, dtype=np.int)
  # \bar{P} &= \underset{i}{\max} \delta_T(i) 
  # \bar{q}_T &= \underset{i}{\arg \max} \delta_T(i) 
  logP = np.max(logdelta[T-1])
  logQ[T-1] = np.argmax(logdelta[T-1])
  # \bar{q}_t = \psi_{t+1}( \bar{q}_{t+1} ) \qquad \text{where} \qquad t=T-1,T-2,\cdots,2,1
  for t in range(T-2, -1, -1):
    logQ[t] = logpsi[t+1, logQ[t+1]]
 
  return logQ, logP

def Prepare_X_GMM(X, Lambda):
  from collections import namedtuple
  PreX = namedtuple('PreX', 'O T alpha beta alpha_hat beta_hat')
  ret = []
  for k in range(len(X)):
    O = X[k]
    T = len(O)
    alpha = Alpha_GMM(O, Lambda)
    beta = Beta_GMM(O, Lambda)
    alpha_hat = Alpha_Hat_GMM(O, Lambda)
    beta_hat = Beta_Hat_GMM(O, Lambda, alpha_hat.C)
    ret.append(PreX(O=O,T=T,alpha=alpha,beta=beta,alpha_hat=alpha_hat,beta_hat=beta_hat))
  return ret

def Baum_Welch_GMM(X, N, L, max_iter=30, epsilon=1e-8):
    # initial state probabilities
    Pi = np.random.dirichlet(np.ones(N), size=1).flatten() # \Pi = [\pi_i]
    # state transition probabilities
    A = np.random.dirichlet(np.ones(N), size=N) # A = [a_{ij}]
    
    # observation emission probabilitity densities
    # dementional
    X_d = len(X[0][0])
    # probability of sepecify gaussian case
    B_coef = np.random.dirichlet(np.ones(L), size=N)
    # gaussian mean
    B_mean = np.random.random(size=[N, L, X_d])
    # gaussian covariance matrix
    B_cov = np.random.random(size=[N, L, X_d, X_d])
    B_cov = np.matmul(B_cov, B_cov.transpose([0,1,3,2]))
    B_cov = B_cov + B_cov.transpose([0,1,3,2])
    
    # the parameters of the model
    Lambda = (A, B_coef, B_mean, B_cov, Pi) # \lambda = (A,B,\Pi)
    
    # total of observations
    X_K = len(X)
    
    pltx, plty, pltz = [], [], []
    
    for it in range(max_iter):
        pre_X = Prepare_X_GMM(X, Lambda)
        
        # probability density for X
        # PDFX = np.prod( [sum([ pre_X[k].alpha(pre_X[k].T-1, i) for i in range(N)]) for k in range(X_K)] )
        # logPDFX = sum( [sum([ np.log( pre_X[k].alpha_hat.C[t] ).sum() for t in range(pre_X[k].T)]) for k in range(X_K)] )
        # np.testing.assert_allclose(PDFX, np.exp(logPDFX), equal_nan=False, err_msg='pdf X')
        
        # PDFXQ = np.prod( [Viterbi(pre_X[k].O, Lambda)[1] for k in range(X_K)] )
        logPDFXQ = np.sum( [logViterbi(pre_X[k].O, Lambda)[1] for k in range(X_K)] )
        # np.testing.assert_allclose(PDFXQ, np.exp(logPDFXQ), equal_nan=False, err_msg='pdf XQ')
        
        pltx.append(it)
        plty.append(logPDFXQ)
        
        # calc initial probabilities
        # Pi_bar = np.zeros(shape=Pi.shape)
        Pi_bar_hat = np.zeros(shape=Pi.shape)
        for i in range(N):
            # Pi_bar[i] = sum([Gamma_GMM(0, i, pre_X[k].O, Lambda, pre_X[k].alpha, pre_X[k].beta) for k in range(X_K)]) / X_K
            Pi_bar_hat[i] = sum([Gamma_Hat_GMM(0, i, pre_X[k].O, Lambda, pre_X[k].alpha_hat, pre_X[k].beta_hat) for k in range(X_K)]) / X_K
        # np.testing.assert_allclose(Pi_bar, Pi_bar_hat, equal_nan=False, err_msg='Pi checking')
        np.testing.assert_allclose(Pi_bar_hat.sum(), 1.0, equal_nan=False, err_msg='s.t. sum of \Pi to 1.0')
        
        # calc transition matrix
        # A_bar = np.zeros(shape=A.shape)
        A_bar_hat = np.zeros(shape=A.shape)
        for i in range(N):
            for j in range(N):
                # A_bar[i, j] = sum([Xi_GMM(t, i, j, pre_X[k].O, Lambda, pre_X[k].alpha, pre_X[k].beta) for k in range(X_K) for t in range(pre_X[k].T-1)]) / sum([Gamma_GMM(t, i, pre_X[k].O, Lambda, pre_X[k].alpha, pre_X[k].beta) for k in range(X_K) for t in range(pre_X[k].T-1)])
                A_bar_hat[i, j] = sum([Xi_Hat_GMM(t, i, j, pre_X[k].O, Lambda, pre_X[k].alpha_hat, pre_X[k].beta_hat) for k in range(X_K) for t in range(pre_X[k].T-1)]) / sum([Gamma_Hat_GMM(t, i, pre_X[k].O, Lambda, pre_X[k].alpha_hat, pre_X[k].beta_hat) for k in range(X_K) for t in range(pre_X[k].T-1)])
        # np.testing.assert_allclose(A_bar, A_bar_hat, equal_nan=False, err_msg='A checking')
        np.testing.assert_allclose(A_bar_hat.sum(axis=1), np.ones(N), equal_nan=False, err_msg='s.t. \sum_j a_ij = 1.0')
        
        # calc B matrix
        # B_bar_coef, B_bar_mean, B_bar_cov = np.zeros(shape=B_coef.shape), np.zeros(shape=B_mean.shape), np.zeros(shape=B_cov.shape)
        B_bar_hat_coef, B_bar_hat_mean, B_bar_hat_cov = np.zeros(shape=B_coef.shape), np.zeros(shape=B_mean.shape), np.zeros(shape=B_cov.shape)
        for i in range(N):
            for l in range(L):
                # B_bar_coef[i, l]  = sum([Gamma_L_GMM(t, i, l, pre_X[k].O, Lambda, pre_X[k].alpha, pre_X[k].beta) for k in range(X_K) for t in range(pre_X[k].T)])
                # B_bar_coef[i, l] /= sum([Gamma_L_GMM(t, i, q, pre_X[k].O, Lambda, pre_X[k].alpha, pre_X[k].beta) for k in range(X_K) for t in range(pre_X[k].T) for q in range(L)])
                
                # B_bar_mean[i, l]  = np.sum([Gamma_L_GMM(t, i, l, pre_X[k].O, Lambda, pre_X[k].alpha, pre_X[k].beta) * pre_X[k].O[t] for k in range(X_K) for t in range(pre_X[k].T)], axis=0)
                # B_bar_mean[i, l] /= sum([Gamma_L_GMM(t, i, l, pre_X[k].O, Lambda, pre_X[k].alpha, pre_X[k].beta) for k in range(X_K) for t in range(pre_X[k].T)])
                
                # B_bar_cov[i, l]  = np.sum([Gamma_L_GMM(t, i, l, pre_X[k].O, Lambda, pre_X[k].alpha, pre_X[k].beta) * np.dot( np.reshape((pre_X[k].O[t] - B_bar_mean[i, l]), [X_d, 1]), np.reshape((pre_X[k].O[t] - B_bar_mean[i, l]), [1, X_d]) ) for k in range(X_K) for t in range(pre_X[k].T)], axis=0)
                # B_bar_cov[i, l] /= sum([Gamma_L_GMM(t, i, l, pre_X[k].O, Lambda, pre_X[k].alpha, pre_X[k].beta) for k in range(X_K) for t in range(pre_X[k].T)])
                
                # for hat
                gamma_i_l = [[Gamma_Hat_L_GMM(t, i, l, pre_X[k].O, Lambda, pre_X[k].alpha_hat, pre_X[k].beta_hat) for t in range(pre_X[k].T)] for k in range(X_K)]
                gamma_i_l_sum = sum([sum(gamma_i_l[k]) for k in range(X_K)])
                
                # coef
                B_bar_hat_coef[i, l]  = gamma_i_l_sum
                
                # mean
                B_bar_hat_mean[i, l] = np.sum([gamma_i_l[k][t] * pre_X[k].O[t] for k in range(X_K) for t in range(pre_X[k].T)], axis=0)
                B_bar_hat_mean[i, l] /= gamma_i_l_sum
                
                # cov
                B_bar_hat_cov[i, l] = np.sum([gamma_i_l[k][t] * np.matmul( np.reshape(pre_X[k].O[t] - B_bar_hat_mean[i, l], [X_d, 1]), np.reshape(pre_X[k].O[t] - B_bar_hat_mean[i, l], [1, X_d]) ) for k in range(X_K) for t in range(pre_X[k].T)], axis=0)
                B_bar_hat_cov[i, l] /= gamma_i_l_sum
                
        B_bar_hat_coef /= np.sum(B_bar_hat_coef, axis=1, keepdims=True)
        
        # np.testing.assert_allclose(B_bar_coef, B_bar_hat_coef, equal_nan=False, err_msg='coef')
        # np.testing.assert_allclose(B_bar_mean, B_bar_hat_mean, equal_nan=False, err_msg='mean')
        # np.testing.assert_allclose(B_bar_cov, B_bar_hat_cov, equal_nan=False, err_msg='cov')
        
        Lambda_bar = (A_bar_hat, B_bar_hat_coef, B_bar_hat_mean, B_bar_hat_cov, Pi_bar_hat)
        diff = np.sqrt(sum([np.square(Lambda_bar[i] - Lambda[i]).sum() for i in range(len(Lambda))]))
        pltz.append(diff)
        
        Lambda = Lambda_bar
        
        print(it, logPDFXQ, diff)
        
        if diff < epsilon:
            break
        
    return Lambda, (pltx, plty, pltz)

# =============================================================================
np.random.seed(42)
# observation sequence
# O = { O_1,O_2,\cdots,O_T } 
# X = \{O^k\}_{k=1}^K
g_X_D = 4
g_X_len_low = 20
g_X_len_high = 30
g_X_K = 35
g_X = [np.random.multivariate_normal(np.random.random(size=g_X_D), np.eye(g_X_D), size=np.random.randint(g_X_len_low, g_X_len_high)) for _ in range(g_X_K)]

# N: number of statesin the model
g_Model_N = 2
# the number of gaussian mixing
g_Model_L = 3

# Baum Welch
Lambda_bar, pltxyz = Baum_Welch_GMM(g_X, g_Model_N, g_Model_L, max_iter=30, epsilon=1e-8)

# testing 
g_O = g_X[0]

g_Q, g_PDFOQ = Viterbi(g_O, Lambda_bar)
g_logQ, g_logPDFOQ = logViterbi(g_O, Lambda_bar)
np.testing.assert_allclose( g_PDFOQ, np.exp( g_logPDFOQ ) ) 

g_PDFOQ = PDFOQ(g_Q, g_O, Lambda_bar)
g_logPDFOQ = logPDFOQ(g_Q, g_O, Lambda_bar)
np.testing.assert_allclose( g_PDFOQ, np.exp( g_logPDFOQ ) )

alpha = Alpha_GMM(g_O, Lambda_bar)
beta = Beta_GMM(g_O, Lambda_bar)
np.testing.assert_allclose( beta.beta[0][0], alpha.alpha[-1].sum() )
np.testing.assert_allclose( alpha.alpha[-1].sum(), sum([alpha(2, i) * beta(3, i) for i in range(g_Model_N)]) )

alpha_hat = Alpha_Hat_GMM(g_O, Lambda_bar)
beta_hat = Beta_Hat_GMM(g_O, Lambda_bar, alpha_hat.C )
np.testing.assert_allclose( alpha.alpha[-1].sum(), np.prod( alpha_hat.C ) )
np.testing.assert_allclose( alpha.alpha[-1].sum(), sum([alpha_hat(1, i) * beta_hat(2, i) * np.prod( alpha_hat.C ) for i in range(g_Model_N)]) )

# show
shifting = 0
plt.subplot(1,2,1)
plt.plot( pltxyz[0][shifting:], pltxyz[1][shifting:] )
plt.title('log viterbi(X)')
plt.xlabel('iter')
plt.ylabel('log viterbi(X)')
plt.subplot(1,2,2)
plt.plot( pltxyz[0][shifting:], pltxyz[2][shifting:] )
plt.title('diff')
plt.xlabel('iter')
plt.ylabel('diff')
plt.show()
# =============================================================================

0 -7087.354061171159 18.581745152990617
1 -5204.931912976656 0.8548144843843375
2 -5153.54691178641 0.5830950886848522
3 -5126.047050948708 0.5030507653593529
4 -5105.274011193578 0.4436046367611551
5 -5090.158096582353 0.3600060911149254
6 -5079.018933037544 0.28021077183681226
7 -5070.732359450655 0.22988248156099672
8 -5064.437962119374 0.21363280592437056
9 -5059.18254551011 0.2272585115388629
10 -5053.853454296295 0.25076407878942814
11 -5049.180538215929 0.2454115673831218
12 -5044.58614092646 0.1980486669137678
13 -5040.718908658764 0.15030996650190787
14 -5037.029475173185 0.13462583153995095
15 -5032.993484112017 0.14188905693730416
16 -5028.943112234142 0.15918200243303968
17 -5025.016058393451 0.18317863464239617
18 -5021.254030631921 0.22357609275866736
19 -5017.857780075199 0.2986755847375107
20 -5013.397911528508 0.32835242533003234
21 -5009.566010268076 0.19204835060031583
22 -5006.5764218462 0.09665568837033864
23 -5003.874996032923 0.07049132848082566
24 -5001.442887752664 0.061711199974353564
25 -4999.214561662449 0.05751775772948252
26 -4997.066795052535 0.05534578069355525
27 -4995.069743936771 0.054576498257133385
28 -4993.2136027096985 0.05536390565866719
29 -4991.492109116793 0.0587813763199914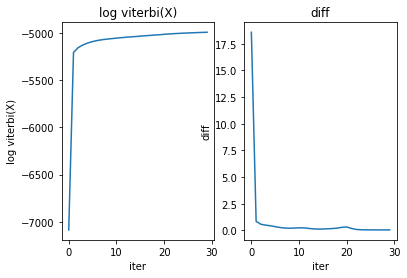

ref:

[1] Rabiner, L. R. 1989. “A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition.” Proceedings of the IEEE 77:257–286.
[2] Steve Renals and Peter Bell, Automatic Speech Recognition— ASR Lectures 4&5 28/31 January 2013
[3] Ethem Alpaydın,Introduction to Machine Learning Third Edition p418-432