4 从观测序列中学习模型参数

4.1 最大期望对数似然

设有\(K\)条观测序列\( ^{[5]} \):

\[ X=\{O^k\}_{k=1}^K \]

模型参数\( ^{[5]} \):

\[ \lambda = (A,B,\Pi) \]

调整模型参数使得观测序列概率最大化，即可完成参数学习过程\( ^{[1]} \).

\[ \begin{align}
P(X|\lambda) &= \prod_{k=1}^K P(O^k | \lambda) \\
&= \prod_{k=1}^K \sum_Q P(Q, O^k | \lambda) \\
\log P(X|\lambda) &= \sum_{k=1}^K \log P(O^k | \lambda) \\
&= \sum_{k=1}^K \log \sum_Q P(Q, O^k | \lambda)
\end{align} \]

状态序列\( Q \)未知, 如遍历所有状态序列求和, 计算代价太高且太复杂. 改为计算对数期望. 并在后续简化计算.

Baum-Welch 算法:

\[ \begin{align}
Q(\lambda, \bar{\lambda}) &= \sum_{k=1}^K \sum_Q P(Q|O^k, \lambda) \log P(Q, O^k |\bar{\lambda}) \\
\bar{\lambda} &= \arg \max_{\bar{\lambda}} Q(\lambda, \bar{\lambda})
\end{align} \]

\( Q \)状态概率未知(此时还不存在最佳模型参数), 使用交替迭代的方式计算，第一步随机生成模型参数\( \lambda \)，使用此参数在观测序列上计算得到期望值，再调整参数\( \bar{\lambda} \)使得\( Q(\lambda, \bar{\lambda}) \)最大化， 反复迭代. 最终收敛到极值.

4.1.1 对数概率期望

\[ \begin{align}
\bar{\lambda} &= \arg \max_{\bar{\lambda}} Q(\lambda, \bar{\lambda}) \\
& \Rightarrow \sum_{k=1}^K \sum_Q P(Q|O^k, \lambda) \log P(Q, O^k |\bar{\lambda}) \\
& \Rightarrow \sum_{k=1}^K \sum_Q P(Q|O^k, \lambda) \log \left[ \bar{\pi}_{q_1} \bar{b}_{q_1}(O_1^k) \bar{a}_{q_1 q_2} \bar{b}_{q_2}(O_2^k) \cdots \bar{a}_{q_{t-1} q_T} \bar{b}_{q_T}(O_T^k) \right] \\
& \Rightarrow \left[ \sum_{k=1}^K \sum_Q P(Q|O^k, \lambda) \log \bar{\pi}_{q_1} \right] + \left[ \sum_{k=1}^K \sum_Q \sum_{t=1}^{T_{O^k}-1} P(Q|O^k, \lambda) \log \bar{a}_{q_t q_{t+1}} \right] + \left[ \sum_{k=1}^K \sum_Q \sum_{t=1}^{T_{O^k}} P(Q|O^k, \lambda) \log \bar{b}_{q_t}(O_t^k) \right]
\end{align} \]

于是，在这里\( \bar{A}, \bar{B}, \bar{\Pi} \)参数被分为三组互相无关的求和，可分别计算最大化\( ^{[3][4]} \).

4.1.2 最大化

\[ \begin{align}
\bar{\Pi} &= \arg \max_{\bar{\Pi}} \sum_{k=1}^K \sum_Q P(Q|O^k, \lambda) \log \bar{\pi}_{q_1} \\
& \Rightarrow \sum_{k=1}^K \sum_{q_1} \sum_{q_2 q_3 \cdots q_{T_{O^k}}} P(q_1 q_2 \cdots q_{T_{O^k}} |O^k, \lambda) \log \bar{\pi}_{q_1} \\
& \Rightarrow \sum_{k=1}^K \sum_{i=1}^N P(q_1 = S_i |O^k, \lambda) \log \bar{\pi}_i \\
& s.t. \sum_{i=1}^N \bar{\pi}_i = 1 \text{ Lagrange Multiplier } \\
& \Rightarrow \max \sum_{k=1}^K \sum_{i=1}^N P(q_1 = S_i |O^k, \lambda) \log \bar{\pi}_i + \mu \left[ \sum_{i=1}^N \bar{\pi}_i – 1 \right] \\
& \Rightarrow \frac{\partial}{\partial \bar{\pi}_i} \sum_{k=1}^K \sum_{i=1}^N P(q_1 = S_i |O^k, \lambda) \log \bar{\pi}_i + \mu \left[ \sum_{i=1}^N \bar{\pi}_i – 1 \right] = 0 \\
& \Rightarrow \frac{\sum_{k=1}^K P(q_1 = S_i |O^k, \lambda)}{\bar{\pi}_i} + \mu = 0 \\
& \Rightarrow \sum_{k=1}^K P(q_1 = S_i |O^k, \lambda) + \mu \bar{\pi}_i = 0 \\
& \Rightarrow \sum_{i=1}^N \left[ \sum_{k=1}^K P(q_1 = S_i |O^k, \lambda) + \mu \bar{\pi}_i \right] = 0 \\
\text{note:} \\
& \frac{\partial}{\partial \mu} \sum_{k=1}^K \sum_{i=1}^N P(q_1 = S_i |O^k, \lambda) \log \bar{\pi}_i + \mu \left[ \sum_{i=1}^N \bar{\pi}_i – 1 \right] = \sum_{i=1}^N \bar{\pi}_i – 1 = 0 \\
\text{so:} \\
& \Rightarrow \sum_{k=1}^K \sum_{i=1}^N P(q_1 = S_i | O^k, \lambda) + \mu \sum_{i=1}^N \bar{\pi}_i = 0 \\
& \Rightarrow K + \mu = 0 \\
& \Rightarrow \frac{\sum_{k=1}^K P(q_1 = S_i |O^k, \lambda)}{\bar{\pi}_i} + \mu = K + \mu \\
{\bar{\pi}_i} &= \frac{\sum_{k=1}^K P(q_1 = S_i |O^k, \lambda)}{K} \\
\bar{A} &= \arg \max_{\bar{A}} \sum_{k=1}^K \sum_Q \sum_{t=1}^{T_{O^k}-1} P(Q|O^k, \lambda) \log \bar{a}_{q_t q_{t+1}} \\
& \Rightarrow \sum_{k=1}^K \sum_{q_t q_{t+1}} \sum_{q_1 \cdots q_{t-1}, q_{t+2} \cdots q_{T_{O^k}}} \sum_{t=1}^{T_{O^k}-1} P(q_1 \cdots q_{t-1},q_t,q_{t+1},q_{t+2} \cdots q_{T_{O^k}}|O^k, \lambda) \log \bar{a}_{q_t q_{t+1}} \\
& \Rightarrow \sum_{k=1}^K \sum_{q_t q_{t+1}} \sum_{t=1}^{T_{O^k}-1} P(q_t,q_{t+1}|O^k, \lambda) \log \bar{a}_{q_t q_{t+1}} \\
& \Rightarrow \sum_{k=1}^K \sum_{i=1}^N \sum_{j=1}^N \sum_{t=1}^{T_{O^k}-1} P(q_t=S_i,q_{t+1}=S_j|O^k, \lambda) \log \bar{a}_{ij} \\
& s.t. \sum_{j=1}^N \bar{a}_{ij} = 1 \text{ Lagrange Multiplier } \\
& \Rightarrow \max \sum_{k=1}^K \sum_{i=1}^N \sum_{j=1}^N \sum_{t=1}^{T_{O^k}-1} P(q_t=S_i,q_{t+1}=S_j|O^k, \lambda) \log \bar{a}_{ij} + \sum_{i=1}^N \mu_i \left[ \sum_{j=1}^N \bar{a}_{ij} – 1 \right] \\
& \Rightarrow \frac{\partial}{\partial \bar{a}_{ij}} \sum_{k=1}^K \sum_{i=1}^N \sum_{j=1}^N \sum_{t=1}^{T_{O^k}-1} P(q_t=S_i,q_{t+1}=S_j|O^k, \lambda) \log \bar{a}_{ij} + \sum_{i=1}^N \mu_i \left[ \sum_{j=1}^N \bar{a}_{ij} – 1 \right] = 0 \\
& \Rightarrow \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}-1} P(q_t=S_i,q_{t+1}=S_j|O^k, \lambda)}{\bar{a}_{ij}} + \mu_i = 0 \\
& \Rightarrow \sum_{k=1}^K \sum_{t=1}^{T_{O^k}-1} P(q_t=S_i,q_{t+1}=S_j|O^k, \lambda) + \mu_i \bar{a}_{ij} = 0 \\
& \Rightarrow \sum_{j=1}^N \left[ \sum_{k=1}^K \sum_{t=1}^{T_{O^k}-1} P(q_t=S_i,q_{t+1}=S_j|O^k, \lambda) + \mu_i \bar{a}_{ij} \right] = 0 \\
\text{note:} \\
& \frac{\partial}{\partial \mu_i } \sum_{k=1}^K \sum_{i=1}^N \sum_{j=1}^N \sum_{t=1}^{T_{O^k}-1} P(q_t=S_i,q_{t+1}=S_j|O^k, \lambda) \log \bar{a}_{ij} + \sum_{i=1}^N \mu_i \left[ \sum_{j=1}^N \bar{a}_{ij} – 1 \right] = \sum_{j=1}^N \bar{a}_{ij} – 1 = 0 \\
\text{so:} \\
& \Rightarrow \sum_{k=1}^K \sum_{t=1}^{T_{O^k}-1} \sum_{j=1}^N P(q_t=S_i,q_{t+1}=S_j|O^k, \lambda) + \mu_i \sum_{j=1}^N \bar{a}_{ij} = 0 \\
& \Rightarrow \sum_{k=1}^K \sum_{t=1}^{T_{O^k}-1} P(q_t=S_i|O^k, \lambda) + \mu_i = 0 \\
& \Rightarrow \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}-1} P(q_t=S_i,q_{t+1}=S_j|O^k, \lambda)}{\bar{a}_{ij}} + \mu_i = \sum_{k=1}^K \sum_{t=1}^{T_{O^k}-1} P(q_t=S_i|O^k, \lambda) + \mu_i \\
\bar{a}_{ij} &= \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}-1} P(q_t=S_i,q_{t+1}=S_j|O^k, \lambda)}{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}-1} P(q_t=S_i|O^k, \lambda)} \\
\bar{B} &= \arg \max_{\bar{B}} \sum_{k=1}^K \sum_Q \sum_{t=1}^{T_{O^k}} P(Q|O^k,\lambda) \log \bar{b}_{q_t}(O_t^k) \\
& \Rightarrow \sum_{k=1}^K \sum_{q_t} \sum_{q_1 \cdots q_{t-1}, q_{t+1} \cdots q_{T_{O^k}}} \sum_{t=1}^{T_{O^k}} P(q_1 \cdots q_{t-1}, q_t, q_{t+1} \cdots q_{T_{O^k}}|O^k,\lambda) \log \bar{b}_{q_t}(O_t^k) \\
& \Rightarrow \sum_{k=1}^K \sum_{i=1}^N \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda) \log \bar{b}_i(O_t^k) \\
& \Rightarrow \sum_{k=1}^K \sum_{i=1}^N \sum_{m=1}^M \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda) \log \bar{b}_i(m)1(O_t^k=v_m) \\
& s.t. \sum_{m=1}^M \bar{b}_i(m) = 1 \text{ Lagrange Multiplier } \\
& \Rightarrow \max \sum_{k=1}^K \sum_{i=1}^N \sum_{m=1}^M \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda) \log \bar{b}_i(m)1(O_t^k=v_m) + \sum_{i=1}^N \mu_i \left[ \sum_{m=1}^M \bar{b}_i(m) – 1 \right] \\
& \Rightarrow \frac{\partial}{\partial \bar{b}_i(m)} \sum_{k=1}^K \sum_{i=1}^N \sum_{m=1}^M \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda) \log \bar{b}_i(m)1(O_t^k=v_m) + \sum_{i=1}^N \mu_i \left[ \sum_{m=1}^M \bar{b}_i(m) – 1 \right] = 0 \\
& \Rightarrow \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda) 1(O_t^k=v_m)}{\bar{b}_i(m)} + \mu_i = 0 \\
& \Rightarrow \sum_{k=1}^K \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda) 1(O_t^k=v_m) + \mu_i \bar{b}_i(m) = 0 \\
& \Rightarrow \sum_{m=1}^M \left[ \sum_{k=1}^K \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda) 1(O_t^k=v_m) + \mu_i \bar{b}_i(m) \right] = 0 \\
\text{note:} \\
& \frac{\partial}{ \partial \mu_i } \sum_{k=1}^K \sum_{i=1}^N \sum_{m=1}^M \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda) \log \bar{b}_i(m)1(O_t^k=v_m) + \sum_{i=1}^N \mu_i \left[ \sum_{m=1}^M \bar{b}_i(m) – 1 \right] = \sum_{m=1}^M \bar{b}_i(m) – 1 = 0 \\
\text{so:} \\
& \Rightarrow \sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \sum_{m=1}^M P(q_t=S_i|O^k,\lambda) 1(O_t^k=v_m) + \mu_i \sum_{m=1}^M \bar{b}_i(m) = 0 \\
& \Rightarrow \sum_{k=1}^K \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda) + \mu_i = 0 \\
& \Rightarrow \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda) 1(O_t^k=v_m)}{\bar{b}_i(m)} + \mu_i = \sum_{k=1}^K \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda) + \mu_i \\
\bar{b}_i(m) &= \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda) 1(O_t^k=v_m)}{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda)}
\end{align} \]

于是最终得到了参数更新:

\[\begin{align}
{\bar{\pi}_i} &= \frac{\sum_{k=1}^K P(q_1 = S_i |O^k, \lambda)}{K} \\
\bar{a}_{ij} &= \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}-1} P(q_t=S_i,q_{t+1}=S_j|O^k, \lambda)}{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}-1} P(q_t=S_i|O^k, \lambda)} \\
\bar{b}_i(m) &= \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda) 1(O_t^k=v_m)}{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} P(q_t=S_i|O^k,\lambda)}
\end{align}\]

定义:

\[ \begin{align}
\xi_t(i, j) & \equiv P(q_t=S_i, q_{t+1}=S_j | O, \lambda) \\
&= \frac{P(q_t=S_i, q_{t+1}=S_j, O | \lambda)}{P(O | \lambda)} \\
&= \frac{P(O | q_t=S_i, q_{t+1}=S_j, \lambda)P(q_t=S_i, q_{t+1}=S_j | \lambda)}{P(O | \lambda)} \\
&= \frac{P(O | q_t=S_i, q_{t+1}=S_j, \lambda)P(q_{t+1}=S_j | q_t=S_i, \lambda)P(q_t=S_i | \lambda)}{P(O | \lambda)} \\
&= \frac{P(O_1 \cdots O_t | q_t=S_i, \lambda)P(O_{t+1} | q_{t+1}=S_j, \lambda)P(O_{t+2} \cdots O_T | q_{t+1}=S_j, \lambda)P(q_{t+1}=S_j | q_t=S_i, \lambda)P(q_t=S_i | \lambda)}{P(O | \lambda)} \\
&= \frac{P(O_1 \cdots O_t, q_t=S_i | \lambda)P(O_{t+1} | q_{t+1}=S_j, \lambda)P(O_{t+2} \cdots O_T | q_{t+1}=S_j, \lambda)P(q_{t+1}=S_j | q_t=S_i, \lambda)}{P(O | \lambda)} \\
&= \frac{ \alpha_t(i) a_{ij} b_j(O_{t+1}) \beta_{t+1}(j) }{ \sum_k^N \sum_l^N \alpha_t(k) a_{kl} b_l(O_{t+1}) \beta_{t+1}(l) } \\
\gamma_t(i) & \equiv P(q_t=S_i | O, \lambda) = \sum_{j=1}^N \xi_t(i,j)
\end{align} \]

\( \gamma_T(i) \)计算时会超出序列长度,可以更改为:

\[ \gamma_t(i) = \frac{ \alpha_t(i) \beta_t(i) }{ \sum_l^N \alpha_t(l) \beta_t(l) } \]

于是更新右侧可以改写为\( ^{[1]} \):

\[\begin{align}
{\bar{\pi}_i} &= \frac{\sum_{k=1}^K \gamma_1^k(i)}{K} \\
\bar{a}_{ij} &= \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}-1} \xi_t^k(i, j)}{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}-1} \gamma_t^k(i)} \\
\bar{b}_i(m) &= \frac{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \gamma_t^k(i) 1(O_t^k=v_m)}{\sum_{k=1}^K \sum_{t=1}^{T_{O^k}} \gamma_t^k(i)}
\end{align}\]

4.1.3 停止迭代

当更新前后参数差小于特定值时停止迭代,模型参数学习完成.

\[ || \lambda – \bar{\lambda} ||_1 < \epsilon \text{ or } || \lambda – \bar{\lambda} ||_2 < \epsilon \]

4.1.4 局部最优

Baum-Welch算法得到的参数无法保证是全局最优，其效果严重依赖随机初始化参数值，为尽量提高参数优化效果，工程中，需要使用多组随机参数作为Baum-Welch算法初值参数，计算完毕后再择优选择最终得到的最好的参数值.

4.2 数值稳定性

使用\( \alpha_t(i), \beta_t(i) \)时，当观测序列过长，计算过程会超出机器精度，这里需要使用 \( \hat{\alpha}_t(i), \hat{\beta}_t(i) \)替代\( ^{[2]} \).

\[\begin{align}
\hat{\xi}_t(i, j) &= \frac{1}{C_{t+1}} \hat{\alpha}_t(i) a_{ij} b_j(O_{t+1}) \hat{\beta}_{t+1}(j) \\
\hat{\gamma}_t(i) &= \hat{\alpha}_t(i) \hat{\beta}_t(i)
\end{align}\]

4.3 代码试验

import numpy as np
from matplotlib import pyplot as plt

np.random.seed(42)

# normal forward algorithm
class Alpha:
  def __init__(self, O, Lambda):
    self.O = O
    self.A, self.B, self.Pi = Lambda
    self.T = len(O)
    self.N = self.A.shape[0]
    self.M = self.B.shape[1]
    assert( self.A.shape[0] == self.A.shape[1] == self.B.shape[0] == self.Pi.shape[0] )
    assert( min(self.O) >= 0 and max(self.O) < self.B.shape[1] )
    '''
    \alpha_t(i) \equiv P(O_1 \cdots O_t, q_t = S_i | \lambda)
    notice: param t: 0=>t1, 1=>t2, ..., T-1=>T
    '''
    self.alpha = np.zeros(shape=(self.T, self.N))
    for t in range(self.T):
      if t == 0:
        self.alpha[t] = [self.Pi[i] * self.B[i, self.O[t]] for i in range(self.N)]
      else:
        self.alpha[t] = [sum([self.alpha[t-1, h] * self.A[h, i] for h in range(self.N)]) * self.B[i, self.O[t]] for i in range(self.N)]
 
  def __call__(self, t, i):
    return self.alpha[t, i]

# scaling forward algorithm
class Alpha_Hat:
  def __init__(self, O, Lambda):
    self.O = O
    self.A, self.B, self.Pi = Lambda
    self.T = len(O)
    self.N = self.A.shape[0]
    self.M = self.B.shape[1]
    assert( self.A.shape[0] == self.A.shape[1] == self.B.shape[0] == self.Pi.shape[0] )
    assert( min(self.O) >= 0 and max(self.O) < self.B.shape[1] )
    '''
    \hat{\alpha}_t(i) & \equiv P(q_t = S_i | O_1 \cdots O_t, \lambda)
    notice: param t: 0=>t1, 1=>t2, ..., T-1=>T
    '''
    self.C = np.zeros(shape=(self.T,))
    self.alpha_hat = np.zeros(shape=(self.T, self.N))
    for t in range(self.T):
      if t==0:
        self.alpha_hat[t] = [self.Pi[i] * self.B[i, self.O[t]] for i in range(self.N)]
      else:
        self.alpha_hat[t] = [sum([self.alpha_hat[t-1, h] * self.A[h, i] for h in range(self.N)]) * self.B[i, self.O[t]] for i in range(self.N)]
      self.C[t] = self.alpha_hat[t].sum()
      self.alpha_hat[t] /= self.C[t]
 
  def __call__(self, t, i):
    return self.alpha_hat[t,i]
  
# normal backword algorithm
class Beta:
  def __init__(self, O, Lambda):
    self.O = O
    self.A, self.B, self.Pi = Lambda
    self.T = len(O)
    self.N = self.A.shape[0]
    self.M = self.B.shape[1]
    assert( self.A.shape[0] == self.A.shape[1] == self.B.shape[0] == self.Pi.shape[0] )
    assert( min(self.O) >= 0 and max(self.O) < self.B.shape[1] )
    '''
    \beta_t(i) \equiv P(O_{t+1} \cdots O_T | q_t = S_i, \lambda)
    notice: param t: T=>T,T-1=>T-1,...,1=>t1,0=>t0
    '''
    self.beta = np.ones(shape=(self.T+1, self.N))
    for t in range(self.T-1, -1, -1):
      if t == 0:
        self.beta[t] = np.array([ self.Pi[j] * self.B[j, self.O[t]] * self.beta[t+1, j] for j in range(self.N)]).sum()
      else:
        self.beta[t] = np.array([ self.A[:,j] * self.B[j, self.O[t]] * self.beta[t+1, j] for j in range(self.N)]).sum(axis=0)
        
  def __call__(self, t, i):
    return self.beta[t, i]

# scaling backward algorithm
class Beta_Hat:
  def __init__(self, O, Lambda, C):
    self.O = O
    self.A, self.B, self.Pi = Lambda
    self.T = len(O)
    self.N = self.A.shape[0]
    self.M = self.B.shape[1]
    self.C = C
    assert( len(self.O) == len(self.C) )
    assert( self.A.shape[0] == self.A.shape[1] == self.B.shape[0] == self.Pi.shape[0] )
    assert( min(self.O) >= 0 and max(self.O) < self.B.shape[1] )
    '''
    \hat{\beta}_t(i) = \frac{ \beta_t(i) }{ \prod_{u=t+1}^T C_u } 
    notice: param t: T=>T,T-1=>T-1,...,1=>t1,0=>t0
    '''
    self.beta_hat = np.ones(shape=(self.T+1, self.N))
    for t in range(self.T-1, -1, -1):
      if t == 0:
        self.beta_hat[t] = np.array([ self.Pi[j] * self.B[j, self.O[t]] * self.beta_hat[t+1, j] for j in range(self.N)]).sum()
      else:
        self.beta_hat[t] = np.array([ self.A[:,j] * self.B[j, self.O[t]] * self.beta_hat[t+1, j] for j in range(self.N)]).sum(axis=0)
      self.beta_hat[t] /= self.C[t]
 
  def __call__(self, t, i):
    return self.beta_hat[t,i]

def Xi(t, i, j, O, Lambda, alpha, beta):
  # \xi_t(i, j) = \frac{ \alpha_t(i) a_{ij} b_j(O_{t+1}) \beta_{t+1}(j) }{ \sum_k^N \sum_l^N \alpha_t(k) a_{kl} b_l(O_{t+1}) \beta_{t+1}(l) }
  A, B, Pi = Lambda
  N, M = B.shape
  numerator = alpha(t, i) * A[i, j] * B[j, O[t+1]] * beta(t+2, j)
  denominator = sum( [alpha(t, i) * A[i, j] * B[j, O[t+1]] * beta(t+2, j) for i in range(N) for j in range(N)] )
  return numerator/denominator

def Xi_Hat(t, i, j, O, Lambda, alpha_hat, beta_hat):
  # \hat{\xi}_t(i, j) &= \frac{1}{C_{t+1}} \hat{\alpha}_t(i) a_{ij} b_j(O_{t+1}) \hat{\beta}_{t+1}(j)
  A, B, Pi = Lambda
  N, M = B.shape
  numerator = alpha_hat(t, i) * A[i, j] * B[j, O[t+1]] * beta_hat(t+2, j)
  denominator = alpha_hat.C[t+1]
  return numerator/denominator

def Gamma(t, i, O, Lambda, alpha, beta):
  # \gamma_t(i) = \frac{ \alpha_t(i) \beta_t(i) }{ \sum_l^N \alpha_t(l) \beta_t(l) }
  A, B, Pi = Lambda
  N, M = B.shape
  numerator = alpha(t, i) * beta(t+1, i)
  denominator = sum( [alpha(t, i) * beta(t+1, i) for i in range(N)] )
  return numerator / denominator

def Gamma_Hat(t, i, O, Lambda, alpha_hat, beta_hat):
  # \hat{\gamma}_t(i) &= \hat{\alpha}_t(i) \hat{\beta}_t(i)
  return alpha_hat(t, i) * beta_hat(t+1, i)

def Prepare_X(X, Lambda):
  from collections import namedtuple
  PreX = namedtuple('PreX', 'O T alpha beta alpha_hat beta_hat')
  ret = []
  for k in range(len(X)):
    O = X[k]
    T = len(O)
    alpha = None # Alpha(O, Lambda)
    beta = None # Beta(O, Lambda)
    alpha_hat = Alpha_Hat(O, Lambda)
    beta_hat = Beta_Hat(O, Lambda, alpha_hat.C)
    ret.append(PreX(O=O,T=T,alpha=alpha,beta=beta,alpha_hat=alpha_hat,beta_hat=beta_hat))
  return ret

def Baum_Welch(X, M, N, max_iter=30, epsilon=1e-8):
  # initial state probabilities
  Pi = np.random.dirichlet(np.ones(N), size=1).flatten() # \Pi = [\pi_i]
  # state transition probabilities
  A = np.random.dirichlet(np.ones(N), size=N) # A = [a_{ij}]
  # observation emission probabilities
  B = np.random.dirichlet(np.ones(M), size=N) # B = [b_j(m)]
  # the parameters of the model
  Lambda = (A, B, Pi) # \lambda = (A,B,\Pi)
  # total of observations
  K = len(X)
  
  pltx, plty, pltz = [], [], []
  
  for it in range(max_iter):
    pre_X = Prepare_X(X, Lambda)
    
    #PX = np.prod( [sum([ pre_X[k].alpha(pre_X[k].T-1, i) for i in range(N)]) for k in range(K)] )
    logPX = sum( [sum([ np.log( pre_X[k].alpha_hat.C[t] ).sum() for t in range(pre_X[k].T)]) for k in range(K)] )
    #np.testing.assert_allclose(PX, np.exp(logPX))
    
    pltx.append(it)
    plty.append(logPX)
    
    # Pi_bar = np.zeros(shape=Pi.shape)
    Pi_bar_hat = np.zeros(shape=Pi.shape)
    for i in range(N):
      # Pi_bar[i] = sum([Gamma(0, i, pre_X[k].O, Lambda, pre_X[k].alpha, pre_X[k].beta) for k in range(K)]) / K
      Pi_bar_hat[i] = sum([Gamma_Hat(0, i, pre_X[k].O, Lambda, pre_X[k].alpha_hat, pre_X[k].beta_hat) for k in range(K)]) / K
    # np.testing.assert_allclose(Pi_bar, Pi_bar_hat)
    np.testing.assert_allclose(Pi_bar_hat.sum(), 1.0)
    
    # A_bar = np.zeros(shape=A.shape)
    A_bar_hat = np.zeros(shape=A.shape)
    for i in range(N):
      for j in range(N):
        # A_bar[i, j] = sum([Xi(t, i, j, pre_X[k].O, Lambda, pre_X[k].alpha, pre_X[k].beta) for k in range(K) for t in range(pre_X[k].T-1)]) / sum([Gamma(t, i, pre_X[k].O, Lambda, pre_X[k].alpha, pre_X[k].beta) for k in range(K) for t in range(pre_X[k].T-1)])
        A_bar_hat[i, j] = sum([Xi_Hat(t, i, j, pre_X[k].O, Lambda, pre_X[k].alpha_hat, pre_X[k].beta_hat) for k in range(K) for t in range(pre_X[k].T-1)]) / sum([Gamma_Hat(t, i, pre_X[k].O, Lambda, pre_X[k].alpha_hat, pre_X[k].beta_hat) for k in range(K) for t in range(pre_X[k].T-1)])
    # np.testing.assert_allclose(A_bar, A_bar_hat)
    np.testing.assert_allclose(A_bar_hat.sum(axis=1), np.ones(N))
    
    # B_bar = np.zeros(shape=B.shape)
    B_bar_hat = np.zeros(shape=B.shape)
    for i in range(N):
      for m in range(M):
        # B_bar[i, m] = sum([Gamma(t, i, pre_X[k].O, Lambda, pre_X[k].alpha, pre_X[k].beta) * (m == pre_X[k].O[t]) for k in range(K) for t in range(pre_X[k].T)]) / sum([Gamma(t, i, pre_X[k].O, Lambda, pre_X[k].alpha, pre_X[k].beta) for k in range(K) for t in range(pre_X[k].T)])
        B_bar_hat[i, m] = sum([Gamma_Hat(t, i, pre_X[k].O, Lambda, pre_X[k].alpha_hat, pre_X[k].beta_hat) * (m == pre_X[k].O[t]) for k in range(K) for t in range(pre_X[k].T)]) / sum([Gamma_Hat(t, i, pre_X[k].O, Lambda, pre_X[k].alpha_hat, pre_X[k].beta_hat) for k in range(K) for t in range(pre_X[k].T)])
    # np.testing.assert_allclose(B_bar, B_bar_hat)
    np.testing.assert_allclose(B_bar_hat.sum(axis=1), np.ones(N))
    
    diff = np.sqrt( np.square(A_bar_hat - Lambda[0]).sum() + np.square(B_bar_hat - Lambda[1]).sum() + np.square(Pi_bar_hat - Lambda[2]).sum() )
    
    pltz.append(diff)
    
    Lambda = (A_bar_hat, B_bar_hat, Pi_bar_hat)
    
    print(it, logPX, diff)
    
    if diff < epsilon:
      break
    
  return Lambda, (pltx, plty, pltz)

# observation sequence
# O = { O_1,O_2,\cdots,O_T } 
# X=\{O^k\}_{k=1}^K
g_X = [[1,2,3,4,5,6],
        [1,2,3],
        [2,3,0,5],
        [5,4,3],
        [5,2]]
# M: number of distinct observation symbols
# N: number of statesin the model
g_M, g_N = 7, 3

Lambda_hat, pltxyz = Baum_Welch(g_X, g_M, g_N, 30, 1e-8)

plt.subplot(1,2,1)
plt.plot( pltxyz[0], pltxyz[1] )
plt.title('log P(X)')
plt.xlabel('iter')
plt.ylabel('log P(X)')
plt.subplot(1,2,2)
plt.plot( pltxyz[0], pltxyz[2] )
plt.title('diff')
plt.xlabel('iter')
plt.ylabel('diff')
plt.show()

输出:

0 -40.62497815989722 0.721147173024104
1 -30.508399927426787 0.354986113329732
2 -28.247689077612087 0.4567153042700449
3 -25.137580719169478 0.34841771603747757
4 -22.822641883753615 0.20386784210766162
5 -21.789989273643144 0.16405469446060156
6 -21.04255296942742 0.07327578135195437
7 -20.671984408468745 0.008848699208315375
8 -20.62369397471953 0.001030852735906072
9 -20.621511230954965 0.00046458927822352956
10 -20.62076650836539 0.00020925707720285193
11 -20.620433631826145 9.418600277596499e-05
12 -20.620284267984392 4.238121825715551e-05
13 -20.620217161942527 1.906868108141107e-05
14 -20.62018699705531 8.579476653362092e-06
15 -20.620173433971743 3.860169682862392e-06
16 -20.620167334511994 1.736846135801057e-06
17 -20.62016459116371 7.814946589306341e-07
18 -20.6201633571643 3.5164095716767247e-07
19 -20.62016280204743 1.5822691384362145e-07
20 -20.620162552310738 7.119794001774433e-08
21 -20.620162439952967 3.2037566706928046e-08
22 -20.620162389400523 1.4416361746859321e-08
23 -20.620162366655006 6.487167112221767e-09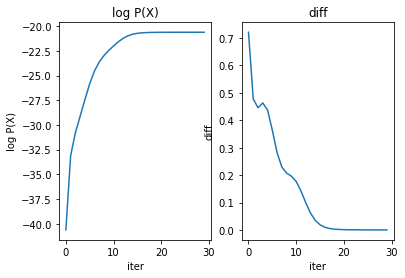

References:
[1] Rabiner, L. R. 1989. “A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition.” Proceedings of the IEEE 77:257–286.
[2] Christopher M. Bishop “Pattern Recognition and Machine Learning” 2006 Springer 13.2.4 Scaling factors p627-629.
[3] Advanced Stochastic Modeling Course material for STA 531
[4] Stephen Tu, Derivation of Baum-Welch Algorithm for Hidden Markov Models
[5] Ethem Alpaydın,Introduction to Machine Learning Third Edition p418-432