2.1 PCFG

概率上下文无法语法是上下文无关语法的简单扩充, 以赋予候选剖析树概率的方式解决原始上下文无关语法的剖析歧义问题.

2.1.1 CFG的概率扩展

1. 非终极符号集合: \( N \)
2. 终极符号集合: \( \Sigma \)
3. 产生式集合\( P \),每个产生式形式为\( A \to \alpha \), 其中\( A \in N \)是单个非终极符号, \( \alpha \)是\(\Sigma \cup N \)组成的符号串。
4. 初始符号: \( S \) 表示句子

概率上下文无关文法相对原始上下文无关文法的改变是给产生式集合\(P\)中的每个规则加上条件概率

\[ A \to \alpha [p] \]

于是原始的上下文无关文法描述变为PCFG五元组 \( G = (N,\Sigma,P,S,D) \), 其中\(D\)就是给\(P\)的所有规则分别指定的概率。

把单个非终极符号\(A\)展开为符号序列\(\alpha\)的概率:

\[ P(A \to \alpha) = P(A \to \alpha | A) \]

使用PCFG给待解析句子S的每个候选剖析树计算概率, 通过比较概率消解剖析歧义，选择概率最大的剖析树为解析结果。

特定剖析树的概率定义为: 在该剖析树中的所有产生式规则概率的乘积

\[ P(T|S) = \prod_{A \to \alpha \in T} p(A \to \alpha) \]

对所有候选剖析树来说,句子S只有一个。因此：

\[ P(T|S) = P(T) \]

我们期望得到给定句子的最佳剖析树

\[ \widehat{T} = \arg\max_{T \in \tau(S) }P(T|S) = \arg\max_{T \in \tau(S)} P(T) \]

\(\tau(S)\) 是被剖析句子的所有剖析树

2.1.2 CYK算法

很显然,不可能把所有候选剖析树概率都计算对比, 考虑到在每个剖析树中的每个产生式是各自独立的.并且从底向上有树形从属关系， CYK(Cocke–Younger–Kasami)就是使用此特点减少计算量的自底向顶的动态规划算法。在PCFG中使用的是概率CYK算法。

2.1.2.1 CNF

CYK算法要求语法满足Chomsky范式, 即每个产生规则最多只能展开两个符号的符号串。在实践中非终极符号展开多于两个符号，需要转换原始句法树为CNF语法,然后再做产生规则学习, 接着再用CYK算法剖析句子, 剖析完成后再转换为原始的句法树。

NLTK带CNF转换, 将展开符号长度超过两个符号的转换为左右规则的CNF语法或逆向转换.

tree.chomsky_normal_form()
tree.un_chomsky_normal_form()
tree.draw()

在CTB样例:
原始树: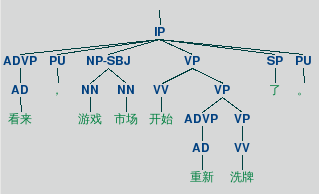

CNF: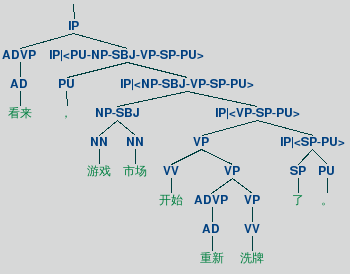

2.1.2.2 CYK代码

由于所有产生规则都是 \(A \to \alpha\) 其中符号串\(\alpha\)最多只有两个符号长度, 用\(B,C\)两个符号替代\(\alpha\)
那么被剖析句子任意子序列\(w_{i \to j}\)都可被剖析为:

\[ \begin{align}
A &\to BC \\
B &\to w_{i \to k} \\
C &\to w_{k+1 \to j} \\
1 &\leq k < n
\end{align} \]

详细算法:

基底:
设长度为1的句子,也就是只有一个词语. 在CNF中给定的非终极符号只有一种可能展开 \( A \to w_i \), 对所有\( A \to w_i \)产生式成立时有 \( A \Rightarrow w_i \), 也就是说,通过非终极符号\( A \),总是推导产生\( w_i \)。

递归:
对词串长度大于1的子句\( w_{ij} \), 产生规则\( A \to BC \), 存在某个\( i \leq k \langle j \), 使得\(B \Rightarrow w_{ik}\)和\(C \Rightarrow w_{kj}\)成立, 于是\(A \Rightarrow w_{ij}\), 使得 \(B\) 推出 \( w_{ik} \), \(C\)推出 \( w_{k+1 \to j} \). 因为\( B,C \)推导的终极符号串和\( A \)推导出的结果相同. 且它们已经被存储在之前推导得到的矩阵中\( \pi \)中, 于是我们把概率\( p(A \to BC) \)乘存储在\(\pi\)中之前计算得到的\(p(B \Rightarrow w_{ik}) p(C \Rightarrow w_{k+1 \to j})\)的概率.就得到了最新的\( A \Rightarrow w_{ij} \)的概率. 因为\( A \to BC \)的产生规则有很多.所以只取候选产生式中概率最大的.也就是说在所有可能的\(k,A,B,C\)中选择最大概率的值.

伪代码:
function CYK(words, grammar) return best_parse}
\(\quad\)Create and clear \(\pi[num\_words, num\_words, num\_nonterminals]\)}

\(\quad \text{#}\)base case
\(\quad\)for \(i = 1\) to num_words
\(\quad \quad\)for \(A = 1\) to num_nonterminals
\(\quad \quad \quad\)if \(A \to w_i\) is in grammar then
\(\qquad \quad \quad \quad \pi[1,i,A] = p(A \to w_i)\)

\(\quad \text{#}\)recursive case
\(\quad\)for \(j=2\) to num_words
\(\quad \quad\)for \(i = 1\) to \(num\_words-j+1\)
\(\quad \quad \quad\)for \(k = 1\) to \(j-1\)
\(\quad \quad \quad \quad\)for \(A = 1\) to num_nonterminals
\(\quad \quad \quad \quad\)for \(B = 1\) to num_nonterminals
\(\quad \quad \quad \quad\)for \(C = 1\) to num_nonterminals
\(\quad \quad \quad \quad \quad prob = \pi[k,j,B] \times \pi[j-k, i+k, C] \times p(A \to BC)\)
\(\quad \quad \quad \quad \quad\)if \(prob > \pi[i,j,A]\) then
\(\quad \quad \quad \quad \quad \quad \pi[i,j,A]=prob\)
\(\quad \quad \quad \quad \quad \quad back[i,j,A]=\{k,B,C\}\)

\( back \)保存了剖析树的反向指针数组，用于逆向（自顶向下）取出剖析结果树。

\(\pi[x,y,z]=p\)中,\(x\)是子句长度，\(y\)是子句开始位置，\(z\)是非终结符号，\(\)p\(\)是概率。

2.1.2.3 学习

算法中需要学习的参数是产生式集合中的每个产生规则概率，可通过统计标记语料得到经验值。

\[ P(A \to \alpha) = \frac{Count(A \to \alpha)}{\sum_{\alpha} Count(A \to \alpha)} = \frac{Count(A \to \alpha)}{Count(\alpha)} \]

2.1.3 Earley算法

CYK算法要求转换为CNF语法规则, Earley可以不转换句法产生式到CNF，而是通过自顶向下和自下向上的方式从左到右分析语句得到完全句法结构，当然对于产生式文法不完善的情况很可能产生空树，且不便于做词汇化概率分析。

2.1.3.1 原始Earley

对于原始Earley算法，会在整个chart中保存所有的完成的或未完成的状态，对剖析，需要在earley的每个状态中增加一个该状态的父状态标号，已便于完成后回溯得到完整的句法树。剖析得到的结果可能是多个树。

2.1.3.2 概率化Earley

原始Earley剖析结果是多个树，但是每个树概率是不同的，我们只需要选取最大概率树，因为文法局部独立，这里就和HMM类似，在每个状态中增加前向概率和内部概率，前向概率用于筛选输入中的合法前缀。内部概率用于排序局部子树，结合viterbi得到最大概率剖析结果。但是在实际应用中还是CYK算法，原因是CYK自底向上的过程容易为每个成份附着中心词。 要详细了解概率化Earley，可参考链接: An Efficient Probabilistic Context-Free Parsing Algorithm that Computes Prefix Probabilities.

2.2 LPCFG

词汇化概率上下文无关语法,给每个成份标签安排一个中心词.这是扩展自CYK算法。在之前的算法中，每次匹配产生式符号时，均匹配到词类就结束, 很显然这并不合理，实际上每个词类下还对应具体的终结符词汇。而这些词汇很可能对句法结构有很大的关系。也就是说对于非词汇化的算法其粒度太粗。通过给句法成份附着句子中的中心意义词汇的方法，辅助句法剖析得到更符合句子内容的句法剖析结果。其算法和概率化CYK没有太大区别，只是在自底向上中按预定规则指定成份中心词，并且平滑因此带来的概率样本缺乏（在样本中很可能并不存在对应成份和中心词联合的产生概率）。

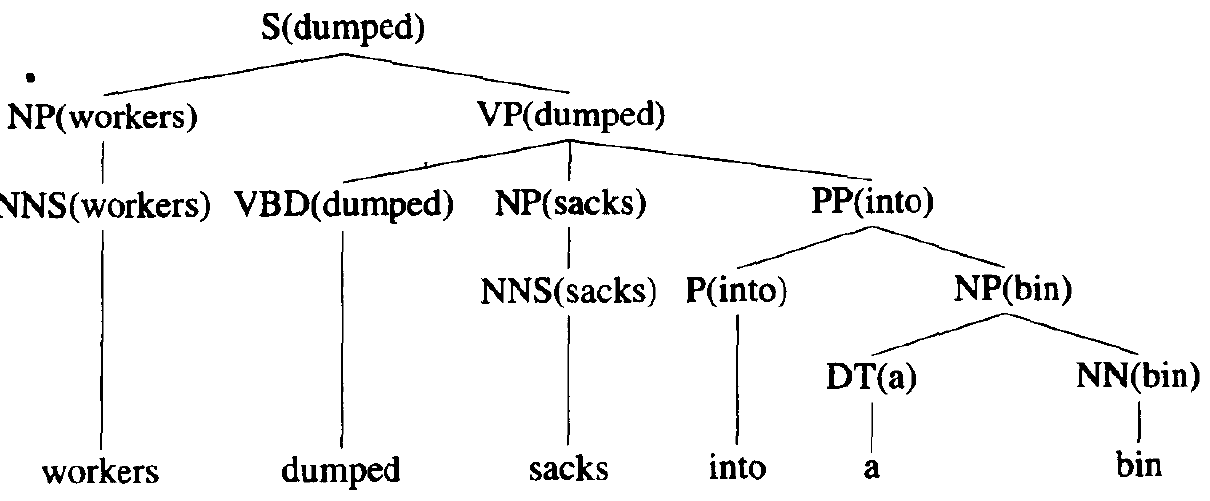
在CTB语料中. Stanford (PCFG) is 72.4%, Stanford (Factored) is 74.4%, Berkeley is 74%. 句子长度大于60时,准确率甚至不到43%.

参考:
1. Daniel Jurafsky, James H. Martin : Speech and Language Processing
2. NLTK
3. Chinese Treebank 8.0
4. 项炜,金澎 :大规模语料库上的 Stanford 和 Berkeley 句法分析器性能对比分析
5. wiki CYK algorithm
6. An Efficient Probabilistic Context-Free Parsing Algorithm that Computes Prefix Probabilities