http://web.stanford.edu/class/psych209/Readings/GravesWayne16DNC.pdf

ARTICLE

doi:10.1038/nature20101

---

Hybrid computing using a neural network with dynamic external memory

Alex Graves\(^1\)*, Greg Wayne\(^1\)*, Malcolm Reynolds\(^1\), Tim Harley\(^1\), Ivo Danihelka\(^1\), Agnieszka Grabska-Barwińska\(^1\), Sergio Gómez Colmenarejo\(^1\), Edward Grefenstette\(^1\), Tiago Ramalho\(^1\), John Agapiou\(^1\), Adrià Puigdomènech Badia\(^1\), Karl Moritz Hermann\(^1\), Yori Zwols\(^1\), Georg Ostrovski\(^1\), Adam Cain\(^1\), Helen King\(^1\), Christopher Summerfield\(^1\), Phil Blunsom\(^1\), Koray Kavukcuoglu\(^1\) & Demis Hassabis\(^1\)

\(^1\)Google DeepMind, 5 New Street Square, London EC4A 3TW, UK
*These authors contributed equally to this work.

Artificial neural networks are remarkably adept at sensory processing, sequence learning and reinforcement learning, but are limited in their ability to represent variables and data structuresand to storedata over long timescales, owing to the lack of an external memory. Here we introduce a machine learning model called to a differentiable neural computer (DNC), which consists of a nerual network that can read from and write to an external memory matrix, analogous to the random-access memory in a conventional computer. Like a conventional computer, it can use its memory to represent and manipulate complex data structures, but , like a nerual network, it can learn to do so from data. When Trained with supervised learning, we demonstrate that a DNC can successfully answer synthetic questions designed to emulate reasoning and inference problems in natural language. We show that it can learn tasks such as finding the shortest path between specified points and inferring the missing links in randomly generated graphs, and then generalize these tasks to specific graphs such as transport networks and family trees. When trained with reinforcement learning, a DNC can complete a moving blocks puzzle in which changing goals are specified by sequences of symbols. Taken together, our results demonstrate that DNCs have the capacity to solve complex, structured tasks that are inaccessible to neural networks without external read-write memory.

Modern computers separate computation and memory. Computation is performed by a processor, which can use an addressable memory to bring operands in and out of play. This confers two important benefits: the use of extensible storage to write new information and the ability to treat the contents of memory as variables. Variables are critical to algorithm generality: to perform the same procedure on one datum or another, an algorithm merely has to change the address it reads from. In contrast to computers, the computational and memory resources of artificial nerual networks are mixed together in the network weights and neuron activity. This is a major liability: as the memory demands of a task increase, these networks cannot allocate new storage dynamically, nor easily learn algorithms that act independently of the values realized by the task variables.

Although recent breakthroughs demonstrate that neural networks are remarkably adept at sensory processing\(^1\), sequence learning\(^{2,3}\) and reinforcement learning\(^4\), cognitive scientists and neuroscientists have argued that neural networks are limited in their ability to represent variables and data structures\(^{5-9}\), and to store data over long timescales without interference\(^{10,11}\). We aim to combine the advantages of neural and computational processing by providing a neural network with read-write access to external memory. The access is narrowly focused, minimizing interference among memoranda and enabling long-term storage\(^{12,13}\). The whole system is differentiable, and can therefore be trained end-to-end with gradient descent, allowing the network to learn how to operate and organize the memory in a goal-directed manner.

System overview

A DAC is a neural network coupled to an external memory matrix. (The behaviour of the network is independent of the memory size as long as the memory is not filled to capacity, which is why we view the memory as ‘external’.) If the memory can be thought of as the DNC’s RAM, then the network, referred to as the ‘controller’, is a differentiable CPU whose operations are learned with gradient descent. The DNC architecture differs from recent neural memory frameworks\(^{14,15}\) in that the memory can be selectively written to as well as read, allowing iterative modification of memory content. An earlier form of DNC, the neural Turing machine\(^{16}\), had a similar structure, but more limited memory access methods (see Methods for further discussion).

Whereas conventional computers use unique addresses to access memory contents, a DNC uses differentiable attention mechanisms \( ^{2,16-18} \) to define distributions over the \( N \) rows, or ‘locations’, in the \( N \times W \) memory matrix \( M \). These distributions, which we call weightings, represent the degree to which each location is involved in a read or write operation. The read vector \( r \) returned by a read weighting \( w^r \) over memory \(M\) is a weighted sum over the memory locations: \( r=\sum^N_{i=1}M\left[i,\cdot\right] w^r \left[i\right] \), where the ‘\( \cdot \)‘ denotes all \( j = 1, \dots , W \). Similarly, the write operation uses a write weighting \( w^W \) to first erase with an erase vector \( e \), then add a write vector \( v: M \left[ i , j \right] \gets M \left[ i , j \right] \left( 1 – w^W \left[ i \right] e \left[ j \right] \right) + w^W \left[ i \right] v \left[ j \right] \). The functional units that determine and apply the weightings are called read and write heads. The operation of the heads is illustrated in Fig.1 and summarized below; see Methods for a formal description.

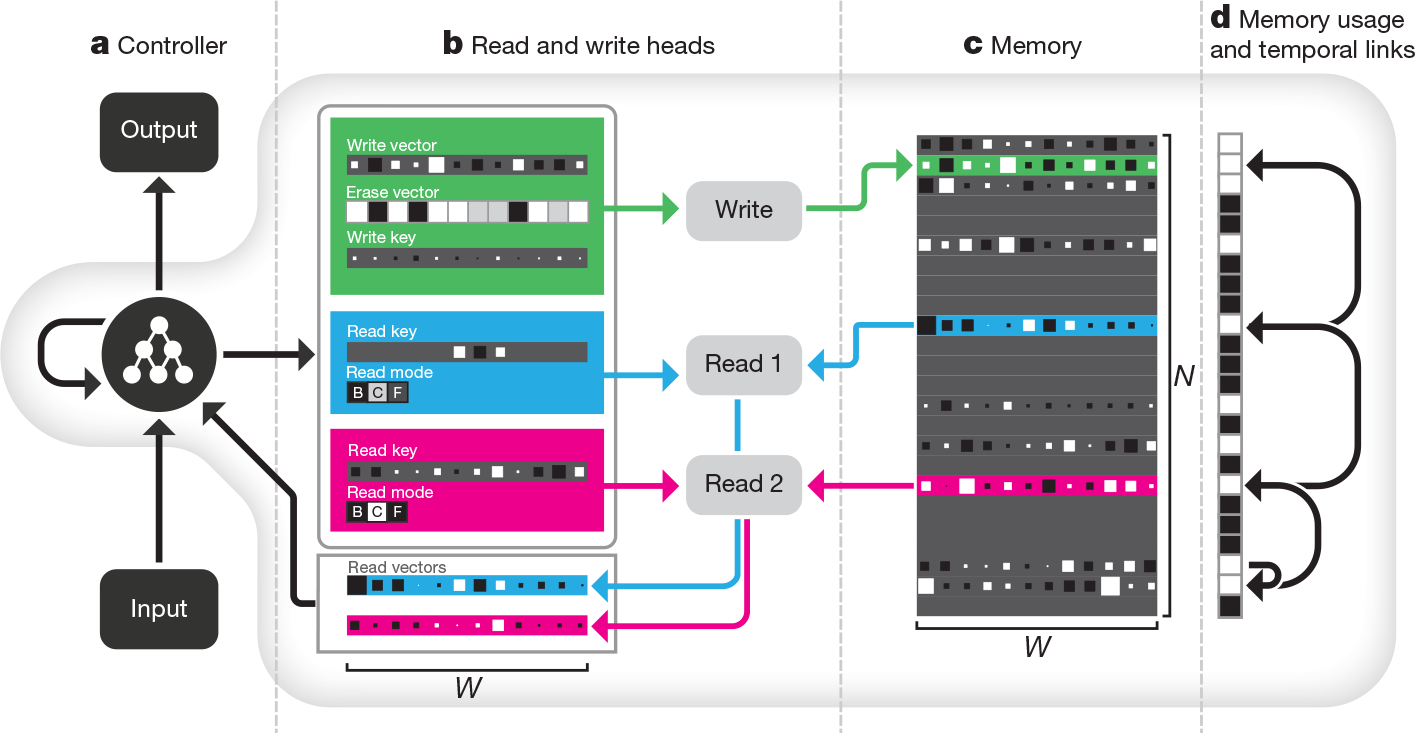
Figure 1 | DNC architecture. a, A recurrent controller network receives input from an external data source and produces output. b, c, The controller also outputs vectors that parameterize one write head(green) and multiple read heads (two in the case, blue and pink). (A reduced selection of parameters is shown.) The write head defines a write and an erase vector that are used to edit the \( N \times W \) memory matrix, whose elements’ magnitudes and signs are indicated by box area and shading, respectively. Additionally, a write key is used for content lookup to find previously written locations to edit. The write key can contribute to defining a weighting that selectively focuses the write operation over the rows, or locations, in the memory matrix. The read heads can use gates called read modes to switch between content lookup using a read key (‘C’) and reading out locations either forwards (‘F’) or backwards (‘B’) in the order they were written. d, The usage vector records which locations have been used so far, and a temporal link matrix records the order in which locations were written; here, we represent the order locations were written to using directed arrows.

Interaction between the heads and the memory

The heads use three distinct forms of differentiable attention. The first is content lookup\( ^{16,17,19-21} \), in which a key vector emitted by the controller is to the content of each location in memory according to a similarity measure (here,cosine similarity). The similarity scores determine a weighting that can be used by the read heads for associative recall\(^{19}\) or by the write head to modify an existing vector in memory. Importantly, a key that only partially matches the content of a memory location can still be uesed to attend strongly to that location. This enables a form of pattern completion whereby the value recovered by reading the memory location includes additional information that is not present in the key. In general, key-value retrieval provides a rich mechanism for navigating associative data structures in the external memory, because the content of one address can effectively encode references to other addresses.

A second attention mechanism records transitions between consecutively written locations in an \( N \times N \) temporal link matrix \(L . L \left[ i , j \right] \) is close to 1 if \( i \) was the next location written after \( j \), and is close to 0 otherwise. For any weighting \( w \), the operation \( Lw \) smoothly shifts the focus forwards to the locations written after those emphasized in \( w \), whereas \( L^Tw \) shifts the focus backwards. This gives a DNC the native ability to recover sequences in the order in which it wrote them, even when consecutive writes did not occur in adjacent time-steps.

The third form of attention allocates memory for writing. The ‘usage’ of each location is represented as a number between 0 and 1, and a weighting that picks out unused locations is delivered to the write head. AS well as automatically increasing with each write to a location, usage can be decreased after each read. This allows the controller to reallocate memory that is no longer required (see Extended Data Fig.1). The allocation mechanism is independent of the size and contents of the memory, meaning that DNCs can be trained to solve a task using one size of memory and later upgraded to a larger memory without retraining (Extended Data Fig.2). In principle, this would make it possible to use an unbounded external memory by automatically increasing the number of locations every time the minimum usage of any location passes a certain threshold.

The design of the attention mechanisms was motivated largely by computational considerations. Content lookup enables the formation of associative data structures; temporal links enable sequential retrieval of input sequences; and allocation provides the write head with unused locations. However, there are interesting parallels between the memory mechanisms of a DNC and the functional capabilities of the mammalian hippocampus. DNC memory modification is fast and can be oneshot, resembling the associative long-term potentiation of hippocampal CA3 and CA1 synapses\(^{22}\). The hippocampal dentate gyrus, a region known to support neurogenesis\(^{23}\), has been proposed to increase representational sparsity, thereby enhancing memory capacity\(^{24}\): usage-based memory allocation and sparse weightings may provide similar facilities in our model. Human ‘free recall’ experiments demonstrate the increased probability of item recall in the same order as first presented-a hippocampus-dependent phenomenon accounted for by the temporal context model\(^{25}\), bearing some similarity to the formation of temporal links(Methods).

Synthetic question answering experiments

Our first experiments investigated the capacity of the DNC to perform question answering. To compare DNCs to other neural network architectures, we considered the bAbI dataset\(^{26}\), which includes 20 types of synthetically generated questions designed to mimic aspects of textual reasoning. The dataset consists of short ‘story’ snippets followed by questions with answers that can be inferred from the stories: for example, the story “John is in the playground. John picked up the football.” followed by the question “Where is the football?” with answer “playground” requires a system to combine two supporting facts, whereas “Sheep are afraid of wolves. Gertrude is a sheep. Mice are afraid of cats. What is Gertrude afraid of?” (answer, “wolves”) tests its facility at basic deduction (and resilience to distractors). We found that a single DNC, jointly trained on all 20 question types with 10,000 instances each, was able to achieve a mean test error rate of 3.8% with task failure(defined as > 5% error) on 2 types of questions, compared to 7.5% mean error and 6 failed tasks for the best previous jointly trained result\(^{21}\). We also found that DNCs performed much better than both long short-term memory\(^{27}\) (LSTM; at present the benchmark neural network for most sequence processing tasks) and the neural Turing machine\(^{16}\) (see Extended Data Table 1 for details). Unlike previous results on the dataset, the inputs to our model were single word tokens without any preprocessing or sentence-level features(see Methods for details).

Graph experiments

Although bAbI is presented in natural language, each declarative sentence involves a limited vocabulary and is generated from a simple triple containing an actor, an action and a set of argumants. Such sentences could easily be rendered in graphical form: for example “John is in the playground” can be diagrammed as two named nodes, ‘Playground’ and ‘John’, connected by a named edge ‘Contains’. In this sense, the propositional knowledge in many of the bAbI tasks is equivalent to a set of constraints on an underlying graph structure. indeed, many important tasks faced by machine learning involve graph data, including parse trees, social networks, knowledge graphs and molecular structures. We therefore turn next to a set of synthetic reasoning experiments on randomly generated graphs.

Unlike bAbI, the edges in our graphs were presented explicitly, with each input vector sepecifying a triple consisting of two node labels and edge label. We generated training graphs with random labelling and conectivity and defined three kinds of query: ‘traversal’,’shortest path’ and ‘inference'(Fig.2). After training with curriculum learning\(^{28,29}\) using graphs and queries with gradually increasing complexity, the networks were tested(with no retraining) on two specific graphs as a test of generalization to realistic data: a symbolic map of the London Underground and an invented family tree.

For the traversal task(Fig.2b), the network was instructed to report the node arrived at after leaving a start and following a path of edges generated by a random walk. For the shortest-path(Fig.2b), a random start and end node were given as the query, and the network was asked to return a sequence of triples corresponding to a minimum-length path between them. Because we considered paths of up to length five, this is a harder version of the path-finding task in the bAbI dataset, which has a maximum length of two. For the inference task(Fig.2c), we predefined 400 ‘relation’ labels that stood as abbreviations for sequences of up to five connected edge labels. A query consisted of an incomplete triple specifying a start node and a relation label, and the required answer was the final node after following the relation sequence. Because the relation sequences were never presented to the network, they had to be inferred fromthe queries and targets.

As a benchmark we again compared DNCs with LSTM. in this case, the best LSTM network we found in an extensive hyper-parameter search failed to complete the first level of its training curriculum of even the easiest task (traversal), reaching an average of only 37% accuracy after almost two million training examples; DNCs reached an average of 98.8% accuracy on the final lesson of the same curriculum after around one million training examples.

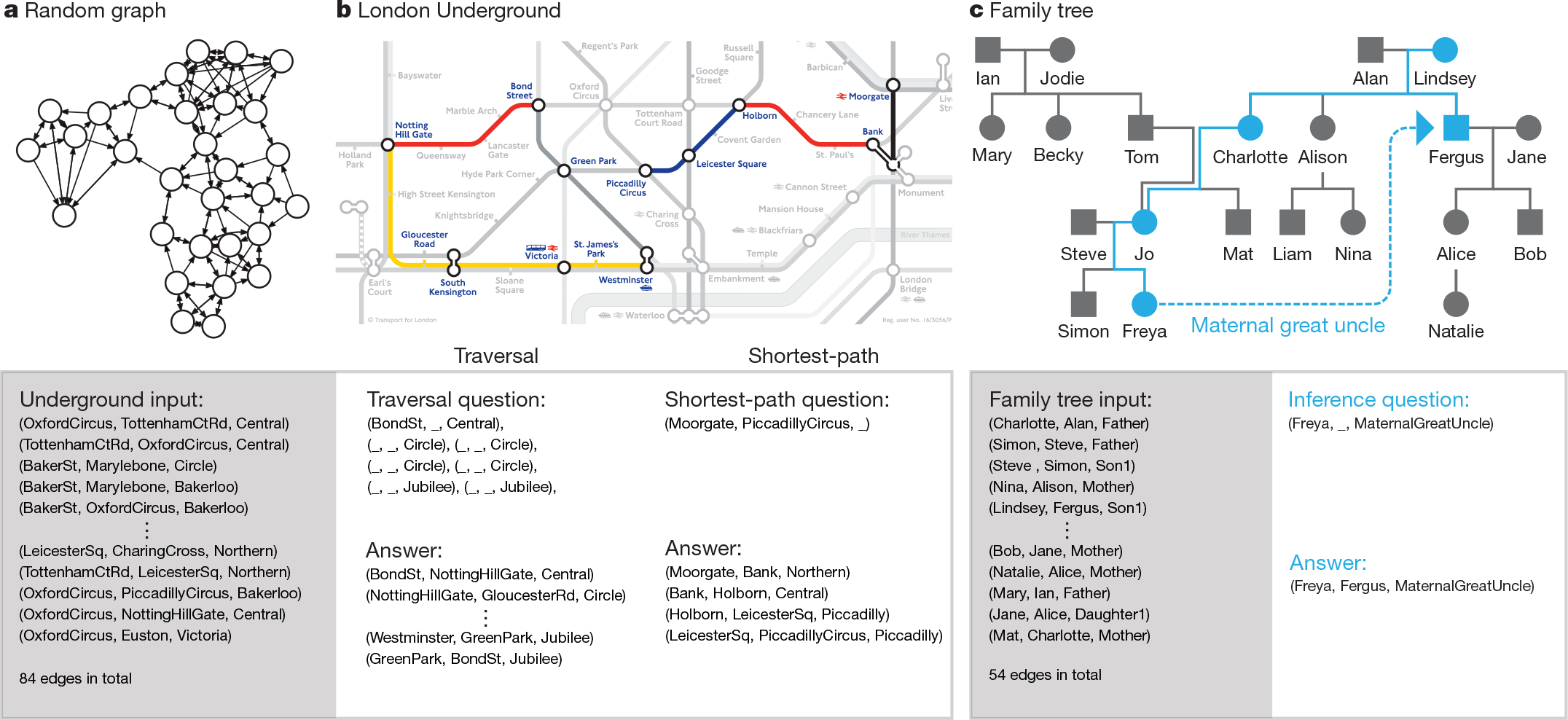
Figure 2 | Graph task. a, An example of a randomly generated graph used for training. b, Zone 1 interchange stations of the Longdon Underground map. used as a generalization test for the traversal and shortest-path tasks. Random seven-step traversals (an example of which is shown on the left) were tested, yielding an average accuracy of 98.8%. Testing on all possible four-step shortest paths (example shown on the right) gave an average accuracy of 55.3%. c, The family tree that was used as a generalization test for the inference task; four-step relations such as the one shown in blue (from Freya to Fergus, her maternal great uncle) were tested, giving an average accuracy of 81.8%. The symbol sequences processed by the network during the test examples are shown beneath the graphs. The input is an unordered list of (‘from node’, ‘to node’, ‘edge’) triple vectors that describes the graph. For each task, the question is a sequence of triples with missing elements (denoted ‘_’) and the answer is a sequence of completed triples.

Figure 3 illustrates a DNC’s use of memory allocation, content lookup and temporal linkage to store and traverse the Longdon Underground map. Visualization of a DNC trained on shortest-path suggests that it progressively explored the links radiating out fromthe start and end nodes until a connectiong path was found(Supplementary Video 1).

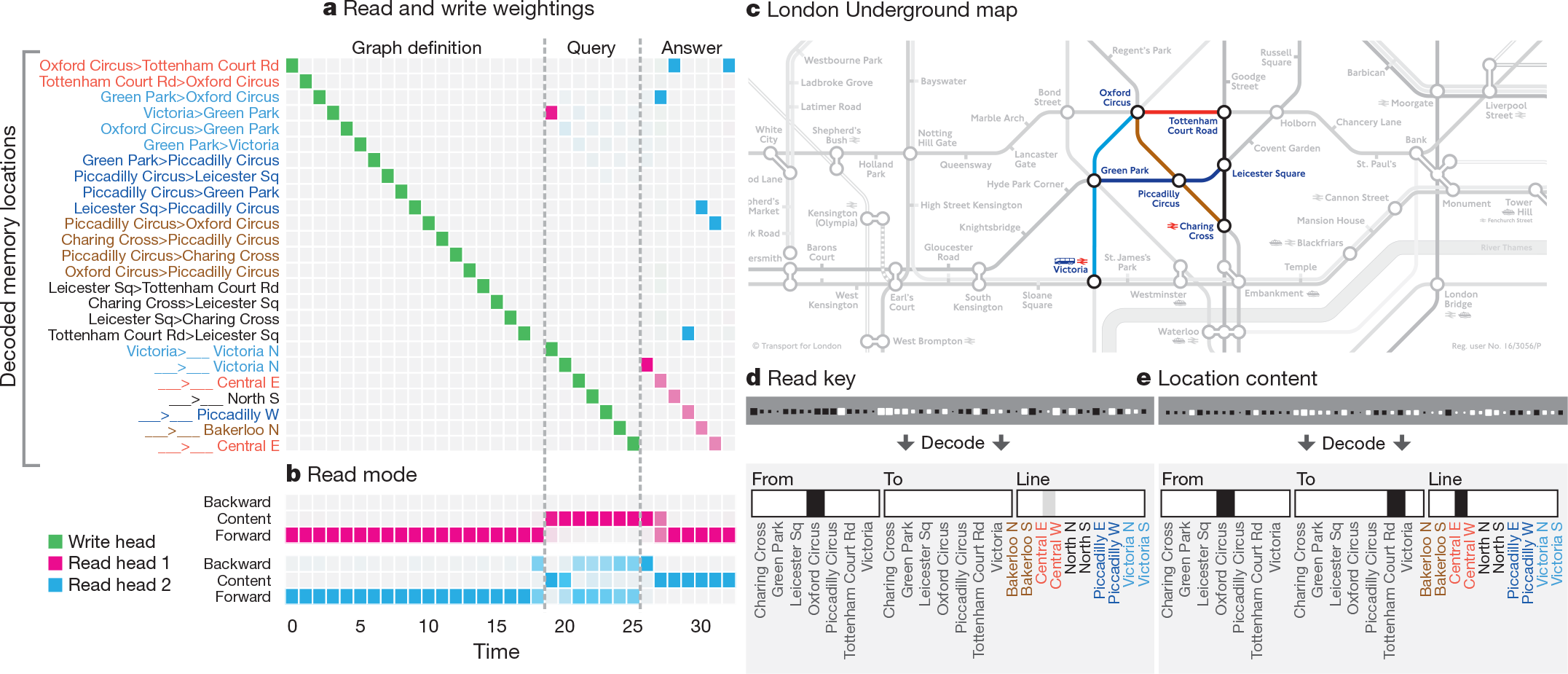
Figure 3 | Traversal on the London Underground. a, During the graph definition phase, the network writes each triple in the map to a separate memory location, as shown by the write weightings(green). During the query phase, the start station (Victoria) and lines to be traversed are recorded. The triple stored in each location can be recovered by a logistic regression decoder, as shown on the vertical axis. b, The read mode distribution during the answer phase reveals that read head 1 (pink) follows temporal links forwards to retrieve the instructions in order, whereas read head 2 (blue) uses content lookup to find the stations along the path. The degree of coloration indicates how strongly each mode is used. c, The region of the map used. d, The final content key used by read head 2 is decoded as a triple with no destination. e, The memory location returned by the key contains the complete triple, allowing the network to infer the destination (Tottenham Court Rd).

Block puzzle experiments

Next we wanted to investigate the ability of DNCs to exploit their memory for logical planning tasks. To do this, we created a block puzzle game inspired by Winograd’s SHRDLU\(^{30}\)-a classic artificial intelligence demonstration of an environment with movable objects and a rule-based agent that executed user instructions. Unlike the previous experiments, for which the networks were trained with supervised learning, we applied a form of reinforcement learning in which a sequence of instructions describing a goal is coupled to a reward function that evaluates whether the goal is satisfied-a set-up that resembles an animal training protocal with a symbolic task cue\(^{31}\).

Our environment, which we term Mini-SHRDLU, contains a set of numbered blocks on a grid board. An agent, given a view of the board as input, can move the top block from a column and deposit it on top of a stack in another column. At every episode, we generated a start board configuration and several possible goals. Each goal, identified by a single-letter label, was composed of several individual constraints on adjacent block paris that were transmitted one constraint per time-step (goal ‘T’ is “block 6 below 2; block 4 left of 1; …”) (Fig.4b,c). After all of the goals were presented, a single goal label was chosen at rondom, and the agent was cued to satisfy that goal.

The DNC used its memory to store the instructions by iteratively writing goals to locations(Fig.4a); it could then carry out any chosen goal(Fig.4c, Supplementary Video 2). We observed that, at the time a goal was written, but many steps before execution was required, the first action could be decoded from memory (Fig.4d). This indicates that the DNC had written its decision to memory before acting upon it; thus, remarkably, DNC learned to make a plan. As with the graph tasks, learning followed a curriculum that gradually increased the number of blocks on the board and constraints in a goal as well as the number of goals and the minimum number of actions needed to find a solution (Methods). Again, the DNC performed substantially better than LSTM (see Fig. 5 and Extended Data Fig. 3).

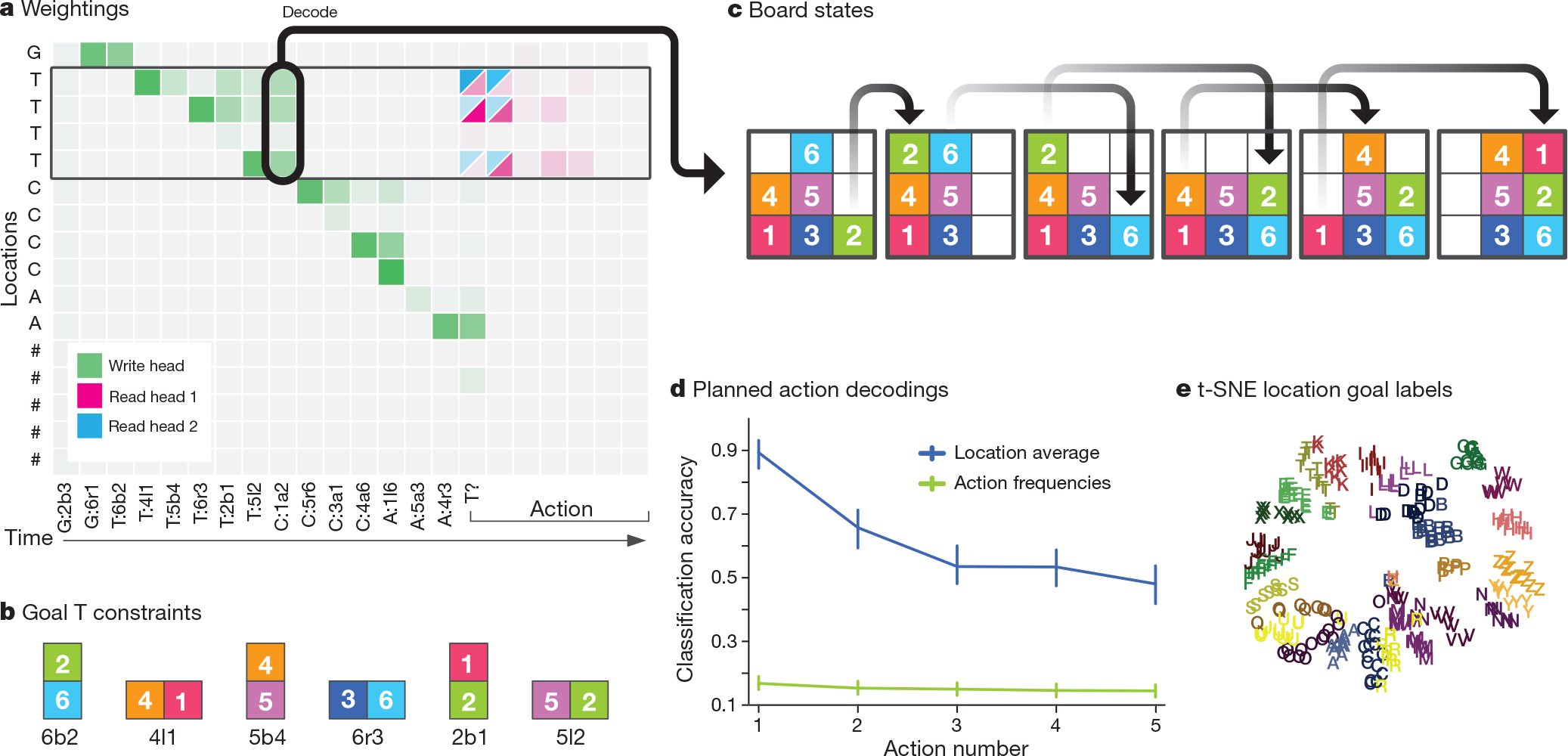
Figure 4 | Mini-SHRDLU analysis. a, In a short example episode, the network wrote goal-related information to sequences of memory locations. (‘G’,’T’,’C’ and ‘A’ denote goals; the numbers refer to the block number; ‘b’,’a’,’l’ and ‘r’ denote ‘below’,’above’,’left of’ and ‘right of’, respectively.) The chosen goal was T (‘T’?), and the read heads focused on the locations containing goal T. b, The constraints comprising goal T. c, The policy made an optimal sequence of moves to satisfy its constraints. d, On 800 random episodes, the first five actions that the network took for the chosen goal were decoded from memory using logistic regression at the time-step after the goal was written (box in a with arrow to c). Decoding accuracy for the first action is 89%, compared to 17% using action frequencies alone, indicating that the network had determined a plan at the time of writing, many steps before execution. Error bars represent 5-95 percentile bootstrapped confidence intervals on validation data. e, Within trials, we average the location contents associated with each goal label into single vectors. Across trials, we create a dataset of there vectors and perform t-SNE(t-distributed stochastic neighbour embedding) dimensionality reduction down to two dimensions. This shows that each goal label is coded geometrically in the memory locations.

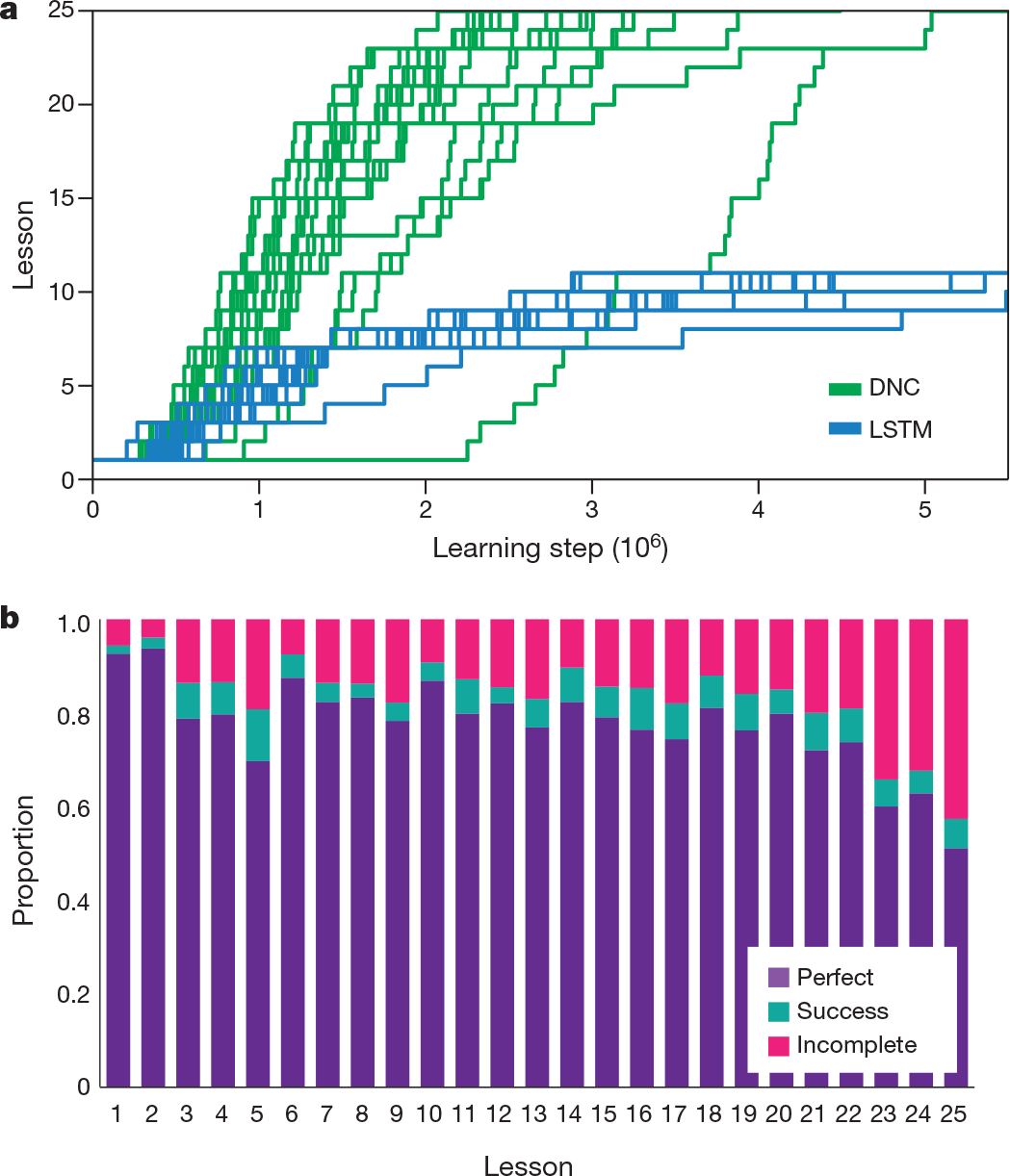
Figure 5 | Mini-SHRDLU results. a, 20 replicated training runs with different random-number seeds for a DNC and LSTM. Only the DNC was able to complete the learning curriculum. b, A single DNC was able to solve a large percentage of problems optimally from each previous lesson (perfect), with a few episodes solved in extra moves (success), and some failures to satisfy all constraints (incomplete).

Discussion

Taken together, the bAbI and graph tasks demonstrate that DNCs are able to process and reason about graph-structured data regardless of whether the links are implicit or explicit. Moreover, we have seen that the structure of the data source is directly reflected in the memory-access procedures learned by the controller. The Mini-SHRDLU problem shows that a systematic use of memory also emerges when a DNC learns by reinforcement to act in pursuit of a set of symbolic goals.

The theme connecting these tasks is the need to learn to represent and reason about the complex, quasi-regular structure embedded in data sequences. In each problem, domain regularities, such as the conventions for representing graphs, are invariant across all sequences shown, on the other hand, for any given sequence, a DNC must detect and capture novel variability as episodic variables in memory. This mixture of large-scale structure and microscopic variability is generic to many problems that confront a cognitive agent\(^{32-34}\). For example, in visual variation in any exemplar. Rooms statistically have chairs in them, but the shape and location of a particular chair in a room are variables. These variable values can be written to the external memory of a DNC, leaving the controller network free to concentrate on learning globle regularities.

Our experiments focused on relatively small-scale synthetic tasks, which have the advantage of being easy to generate and interpret. For such problems, memory matrices of up to 512 locations were sufficient. To tackle real-world data we will need to scale up to thousands or millions of locations, at which point the memory will be able to store more information than can be contained in the weights of the controller. Such systems should be able to continually acquire knowledge through exposure to large, naturalistic data sources, even without adapting network parameters, We aim to further develop DNCs to serve as representational engines for one-shot learning\(^{35-37}\), scene understanding\(^{38}\), language processing\(^{39}\) and cognitive mapping\(^{40}\), capable of intuiting the variable structure and scale of the world with in a single, generic model.

Online Content Methods, along with any additional Extended Data display items and Source Data, are available in the online version of the paper; references unique to these sections appear only in the online paper.

received 5 January; accepted 19 September 2016. Published online 12 October 2016.

1. Krizhevsky, A., Sutskever, I. & Hinton, G. E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems Vol. 25 (eds Pereira, F. et al.) 1097–1105 (Curran Associates, 2012).
2. Graves, A. Generating sequences with recurrent neural networks. Preprint at http://arxiv.org/abs/1308.0850 (2013).
3. Sutskever, I., Vinyals, O. & Le, Q. V. Sequence to sequence learning with neural networks. In Advances in Neural Information Processing Systems Vol. 27 (eds Ghahramani, Z. et al.) 3104–3112 (Curran Associates, 2014).
4. Mnih, V. et al. Human-level control through deep reinforcement learning. Nature 518, 529–533 (2015).
5. Gallistel, C. R. & King, A. P. Memory and the Computational Brain: Why Cognitive Science Will Transform Neuroscience (John Wiley & Sons, 2011).
6. Marcus, G. F. The Algebraic Mind: Integrating Connectionism and Cognitive Science (MIT Press, 2001).
7. Kriete, T., Noelle, D. C., Cohen, J. D. & O’Reilly, R. C. Indirection and symbol-like processing in the prefrontal cortex and basal ganglia. Proc. Natl Acad. Sci. USA 110, 16390–16395 (2013).
8. Hinton, G. E. Learning distributed representations of concepts. In Proc. Eighth Annual Conference of the Cognitive Science Society Vol. 1, 1–12 (Lawrence Erlbaum Associates, 1986).
9. Bottou, L. From machine learning to machine reasoning. Mach. Learn. 94, 133–149 (2014).
10. Fusi, S., Drew, P. J. & Abbott, L. F. Cascade models of synaptically stored memories. Neuron 45, 599–611 (2005).
11. Ganguli, S., Huh, D. & Sompolinsky, H. Memory traces in dynamical systems. Proc. Natl Acad. Sci. USA 105, 18970–18975 (2008).
12. Kanerva, P. Sparse Distributed Memory (MIT press, 1988).
13. Amari, S.-i. Characteristics of sparsely encoded associative memory. Neural Netw. 2, 451–457 (1989).
14. Weston, J., Chopra, S. & Bordes, A. Memory networks. Preprint at http://arxiv.org/abs/1410.3916 (2014).
15. Vinyals, O., Fortunato, M. & Jaitly, N. Pointer networks. In Advances in Neural Information Processing Systems Vol. 28 (eds Cortes, C et al.) 2692–2700 (Curran Associates, 2015).
16. Graves, A., Wayne, G. & Danihelka, I. Neural Turing machines. Preprint at http://arxiv.org/abs/1410.5401 (2014).
17. Bahdanau, D., Cho, K. & Bengio, Y. Neural machine translation by jointly learning to align and translate. Preprint at http://arxiv.org/abs/1409.0473 (2014).
18. Gregor, K., Danihelka, I., Graves, A., Rezende, D. J. & Wierstra, D. DRAW: a recurrent neural network for image generation. In Proc. 32nd International Conference on Machine Learning (eds Bach, F. & Blei, D.) 1462–1471 (JMLR, 2015).
19. Hintzman, D. L. MINERVA 2: a simulation model of human memory. Behav. Res. Methods Instrum. Comput. 16, 96–101 (1984).
20. Kumar, A. et al. Ask me anything: dynamic memory networks for natural language processing. Preprint at http://arxiv.org/abs/1506.07285 (2015).
21. Sukhbaatar, S. et al. End-to-end memory networks. In Advances in Neural Information Processing Systems Vol. 28 (eds Cortes, C et al.) 2431–2439 (Curran Associates, 2015).
22. Magee, J. C. & Johnston, D. A synaptically controlled, associative signal for Hebbian plasticity in hippocampal neurons. Science 275, 209–213 (1997).
23. Johnston, S. T., Shtrahman, M., Parylak, S., Gonc¸ alves, J. T. & Gage, F. H. Paradox of pattern separation and adult neurogenesis: a dual role for new neurons balancing memory resolution and robustness. Neurobiol. Learn. Mem. 129, 60–68 (2016).
24. O’Reilly, R. C. & McClelland, J. L. Hippocampal conjunctive encoding, storage, and recall: avoiding a trade-off. Hippocampus 4, 661–682 (1994).
25. Howard, M. W. & Kahana, M. J. A distributed representation of temporal context. J. Math. Psychol. 46, 269–299 (2002).
26. Weston, J., Bordes, A., Chopra, S. & Mikolov, T. Towards AI-complete question answering: a set of prerequisite toy tasks. Preprint at http://arxiv.org/abs/1502.05698 (2015).
27. Hochreiter, S. & Schmidhuber, J. Long short-term memory. Neural Comput. 9, 1735–1780 (1997).
28. Bengio, Y., Louradour, J., Collobert, R. & Weston, J. Curriculum learning. In Proc. 26th International Conference on Machine Learning (eds Bottou, L. & Littman, M.) 41–48 (ACM, 2009).
29. Zaremba, W. & Sutskever, I. Learning to execute. Preprint at http://arxiv.org/abs/1410.4615 (2014).
30. Winograd, T. Procedures as a Representation for Data in a Computer Program for Understanding Natural Language. Report No. MAC-TR-84 (DTIC, MIT Project MAC, 1971).
31. Epstein, R., Lanza, R. P. & Skinner, B. F. Symbolic communication between two pigeons (Columba livia domestica). Science 207, 543–545 (1980).
32. McClelland, J. L., McNaughton, B. L. & O’Reilly, R. C. Why there are complementary learning systems in the hippocampus and neocortex: insights from the successes and failures of connectionist models of learning and memory. Psychol. Rev. 102, 419–457 (1995).
33. Kumaran, D., Hassabis, D. & McClelland, J. L. What learning systems do intelligent agents need? Complementary learning systems theory updated. Trends Cogn. Sci. 20, 512–534 (2016).
34. McClelland, J. L. & Goddard, N. H. Considerations arising from a complementary learning systems perspective on hippocampus and neocortex. Hippocampus 6, 654–665 (1996).
35. Lake, B. M., Salakhutdinov, R. & Tenenbaum, J. B. Human-level concept learning through probabilistic program induction. Science 350, 1332–1338 (2015).
36. Rezende, D. J., Mohamed, S., Danihelka, I., Gregor, K. & Wierstra, D. One-shot generalization in deep generative models. In Proc. 33nd International Conference on Machine Learning (eds Balcan, M. F. & Weinberger, K. Q.) 1521–1529 (JMLR, 2016).
37. Santoro, A., Bartunov, S., Botvinick, M., Wierstra, D. & Lillicrap, T. Meta-learning with memory-augmented neural networks. In Proc. 33nd International Conference on Machine Learning (eds Balcan, M. F. & Weinberger, K. Q.) 1842–1850 (JMLR, 2016).
38. Oliva, A. & Torralba, A. The role of context in object recognition. Trends Cogn. Sci. 11, 520–527 (2007).
39. Hermann, K. M. et al. Teaching machines to read and comprehend. In Advances in Neural Information Processing Systems Vol. 28 (eds Cortes, C. et al.) 1693–1701 (Curran Associates, 2015).
40. O’Keefe, J. & Nadel, L. The Hippocampus as a Cognitive Map (Oxford Univ. Press, 1978).

Supplementary Information is available in the online version of the paper.

Acknowledgements We thank D. Silver, M. Botvinick and S. Legg for reviewing the paper prior to submission; P. Dayan, D. Wierstra, G. Hinton, J. Dean, N. Kalchbrenner, J. Veness, I. Sutskever, V. Mnih, A. Mnih, D. Kumaran, N. de Freitas, L. Sifre, R. Pascanu, T. Lillicrap, J. Rae, A. Senior, M. Denil, T. Kocisky, A. Fidjeland, K. Gregor, A. Lerchner, C. Fernando, D. Rezende, C. Blundell and N. Heess for discussions; J. Besley for legal assistance; the rest of the DeepMind team for support and encouragement; and Transport for London for allowing us to reproduce portions of the London Underground map.

Author Contributions A.G. and G.W. conceived the project. A.G., G.W., M.R., T.H., I.D., S.G. and E.G. implemented networks and tasks. A.G., G.W., M.R., T.H., A.G.-B., T.R. and J.A. performed analysis. M.R., T.H., I.D., E.G., K.M.H., C.S., P.B., K.K. and D.H. contributed ideas. A.C. prepared graphics. A.G., G.W., M.R., T.H., S.G., A.P.B., Y.Z., G.O. and K.K. performed experiments. A.G., G.W., H.K., K.K. and D.H. managed the project. A.G., G.W., M.R., T.H., K.K. and D.H. wrote the paper.

Author Information Reprints and permissions information is available at www.nature.com/reprints. The authors declare no competing financial interests. Readers are welcome to comment on the online version of the paper. Correspondence and requests for materials should be addressed to A.G. (gravesa@google.com), G.W. (gregwayne@google.com), D.H. (demishassabis@google.com).

Reviewer Information Nature thanks Y. Bengio, J. McClelland and the other anonymous reviewer(s) for their contribution to the peer review of this work.