HMM-1-简介
1 简介
HMM是Hidden Markov Models缩写, 1960s, Baum和他的同事发布一系列论文,1970s CMU的Baker用于实现语音处理,1970s IBM Jelinek和他的同事用于语音处理$^{[1]}$.
重要假设:当前状态仅与上一步状态相关,与上一步之前的状态无关.
1.1 符号定义
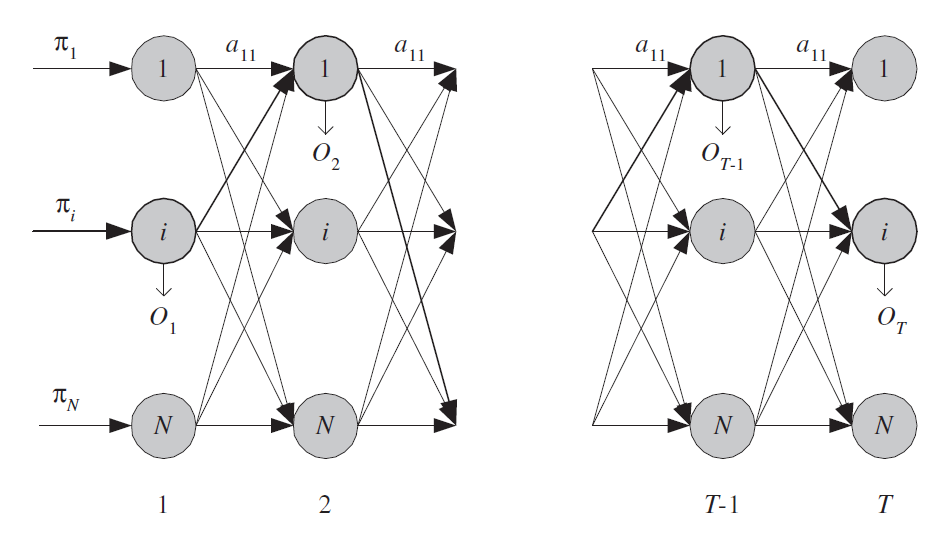
- $ N $:模型状态数量$^{[2]}$.
$$ S = {S_1,S_2,\cdots,S_N} $$ - $ M $:不同观测符号数量$^{[2]}$.
$$ V = {v_1,v_2,\cdots,v_M} $$ $ T $:序列长度$^{[2]}$.
$$ \begin{align} O &= { O_1,O_2,\cdots,O_T } \qquad \text{观测序列} \\ Q &= { q_1,q_2,\cdots,q_T } \qquad \text{状态序列} \\ \end{align} $$
状态转移概率$^{[2]}$:
$$ A = [a_{ij} ] \quad where \quad a_{ij} \equiv P(q_{t+1} = S_j | q_t = S_i) $$
观测概率$^{[2]}$:
$$ B = [b_j(m)] \quad where \quad b_j(m) \equiv P(O_t = v_m | q_t = S_j) $$
初始状态概率$^{[2]}$:
$$ \Pi = [\pi_i] \quad where \quad \pi_i \equiv P(q_1 = S_i) $$
模型参数$^{[2]}$.
$$ \lambda = (A,B,\Pi) $$
1.2 模型
$ \require{AMScd} $
$$ \text{HMM}^{[2]} \\ \begin{CD} q_1 @>>> q_2 @. \cdots @. q_{t-1} @>>> q_t \\ @VVV @VVV @. @VVV @VVV \\ O_1 @. O_2 @. @. O_{t-1} @. O_t \end{CD} \\ P(Q,O | \lambda)=\prod^T_{t=1}p(q_t|q_{t-1}, \lambda)p(O_t|q_t, \lambda) \\ $$
中文分词词性和序列标注之MEMM-1-比较HMM
1.3 数值稳定性
模型计算时存在多个小于1.0的数连乘,最终模型的值将远远低于计算机浮点数最小表达范围.例:
$$ \begin{align} \text{suppose:} T,N,M &= 100,100,1000 \\ \text{subject to:} \sum_{q_t}^N p(q_t|q_{t-1}, \lambda) &= 1.0 \\ \sum_{O_t}^M p(O_t|q_t, \lambda) &= 1.0 \\ \text{thus:} P(Q,O | \lambda) & \approx \left[ \frac{1}{MN} \right] ^T = 1E-500 \end{align} $$
IEEE 754中双精度浮点数精度$^{[3]}$为 $ 2^{53} \approx 1.11 \times 10^{−16} \approx 1E-16$
因此,实践中常用对数概率.
$$ \log P(Q,O | \lambda)=\sum^T_{t=1} \log p(q_t|q_{t-1}, \lambda) + \log p(O_t|q_t, \lambda) $$
1.4 代码试验
import numpy as np
np.random.seed(42)
# T: length of observation
# N: number of statesin the model
# M: number of distinct observation symbols
g_T, g_N, g_M = 10,20,30
# observation sequence
g_O = np.random.randint(low=0, high=g_M, size=g_T).flatten() # O = { O_1,O_2,\cdots,O_T }
# state sequence
g_Q = np.random.randint(low=0, high=g_N, size=g_T).flatten() # Q = { q_1,q_2,\cdots,q_T }
# initial state probabilities
g_Pi = np.random.dirichlet(np.ones(g_N), size=1).flatten() # \Pi = [\pi_i]
# state transition probabilities
g_A = np.random.dirichlet(np.ones(g_N), size=g_N) # A = [a_{ij}]
# observation emission probabilities
g_B = np.random.dirichlet(np.ones(g_M), size=g_N) # B = [b_j(m)]
# the parameters of the model
g_Lambda = (g_A, g_B, g_Pi) # \lambda = (A,B,\Pi)
# the probability of the model given observation sequence and state sequence
def P(Q, O, Lambda):
''' p(Q,O | \lambda)=\prod^T_{t=1}p(q_t|q_{t-1}, \lambda)p(O_t|q_t, \lambda) '''
A, B, Pi = Lambda
T = O.shape[0]
assert( Q.shape == O.shape )
assert( A.shape[0] == A.shape[1] == B.shape[0] == Pi.shape[0] )
assert( Q.min() >= 0 and Q.max() < A.shape[0] )
assert( O.min() >= 0 and O.max() < B.shape[1] )
return np.prod([(A[Q[t-1], Q[t]] if t>0 else Pi[Q[t]]) * B[Q[t],O[t]] for t in range(T)])
# the log probability of the model given observation sequence and state sequence
def logP(Q, O, Lambda):
''' \log P(Q,O | \lambda)=\sum^T_{t=1} \log p(q_t|q_{t-1}, \lambda) + \log p(O_t|q_t, \lambda) '''
A, B, Pi = Lambda
T = O.shape[0]
assert( Q.shape == O.shape )
assert( A.shape[0] == A.shape[1] == B.shape[0] == Pi.shape[0] )
assert( Q.min() >= 0 and Q.max() < A.shape[0] )
assert( O.min() >= 0 and O.max() < B.shape[1] )
logPi, logA, logB = np.log(Pi), np.log(A), np.log(B)
return np.sum([(logA[Q[t-1], Q[t]] if t>0 else logPi[Q[t]]) + logB[Q[t],O[t]] for t in range(T)])
print('P(Q, O) = ', P(g_Q, g_O, g_Lambda))
print('\exp(\log P(Q, O)) = ', np.exp(logP(g_Q, g_O, g_Lambda))
print('\log P(Q, O) = ', logP(g_Q, g_O, g_Lambda) )output: $ \begin{align} P(Q, O) &= 1.3708753719444907e-38 \\ \exp(\log P(Q, O)) &= 1.3708753719444917e-38 \\ \log P(Q, O) &= -87.1827840403565 \end{align} $
References:
[1] Rabiner, L. R. 1989. “A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition.” Proceedings of the IEEE 77:257–286.
[2] Daniel Jurafsky, James H. Martin “Speech and Language Processing” 15.3 Hidden Markov Models :P421
[3] Double-precision floating-point format From Wikipedia