1. 概率无向图模型

概率无向图是指随机变量节点连接边没有方向的概率图模型, 其节点\( v \in V\)表示随机变量，节点之间的边\( e \in E \)表示随机变量之间的依赖关系。

\[ G=(V, E) \]

1.1 团, 最大团

在概率无向图\(G\)中任意两个节点之间均有边连接的子图称为团, 若\(C\)是\(G\)的一个团，且不能再加入\(G\)的任何一个节点组成新团。那么就称\(C\)为最大团.一个图中可以存在多个团或最大团。

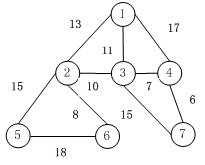
上图：节点{1,2,3}组成一个团，且是最大子团, 但{1,2,3,4}不是一个团，因为{2,4}之间没有直接的边连接。节点{1,2}组成一个团，但它不是最大子团，原因是还可以把节点{3}加入此团。

1.2 马尔可夫网条件独立性

直观观察.概率无向图模型节点之间的依赖性沿着连接边流动。如节点之间无直接边连接且中间节点有确定值，则阻断了对应的依赖性流动。于是节点间条件独立(确定值的节点就是条件)。

下面的三种条件独立描述中，小写字母表示任意单个节点，大写字母表示节点集合。

1.2.1 成对马尔可夫性

设\(u,v\)是无向图G中任意两个没有边连接的节点，对应随机变量\(Y_u, Y_v\)其他所有节点为\(O\),对应随机变量\(Y_O\), 给定\(Y_O\)时, \(Y_u, Y_v\)条件独立。

\[ P(Y_u, Y_v | Y_O) = P(Y_u | Y_O) P(Y_v| Y_O) \]

上图中:节点{1,5}之间没有直接边连接，那么给定节点{2,3,4,6,7}时。节点{1,5}也条件独立的。原因是{1,5}之间的概率依赖流动性被其余节点确定值阻断。

1.2.2 局部马尔可夫性

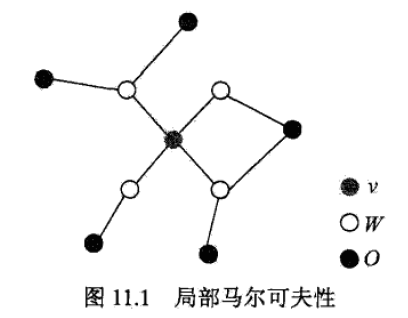
设\(v\)是无向图\(G\)中的任意节点，\(W\)是与\(v\)有边连接的节点.\(O\)是除此以外的其他节点. 在给定\(Y_W\)的情况下，\(Y_v\), \(Y_O\)独立。其实这里和上面的成对独立性是等价，因为确定\(Y_W\)值阻断了随机变量节点\(v\)与\(O\)的依赖性流动。

\[ P(Y_v,Y_O | Y_W) = P(Y_v|Y_W)P(Y_O|Y_W) \]

1.2.3 全局马尔可夫性

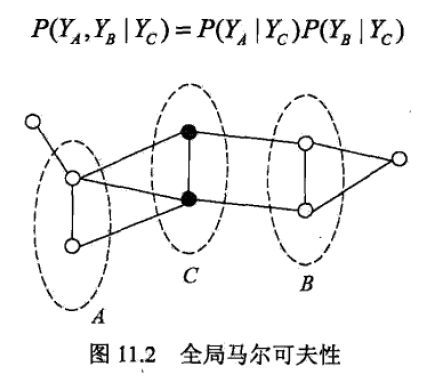
设节点集合\(A,B\)在无向图\(G\)中被节点集合\(C\)分开,其对应随机变量\(Y_A, Y_B, Y_C\)，那么在给定\(Y_C\)时， \(Y_A, Y_B\)条件独立.

成对，局部，全局条件独立定义是等价的。总之就是在无向图中只要节点或节点集合之间没有直接边连接,且中间的依赖性流动边被确定值阻断，那么它们就独立. 只要满足以上条件独立定义，那么就成为概率无向图模型或马尔可夫随机场，且因为存在独立性，那么就可以使用概率求积的形式得到图模型联合概率.

1.3 概率无向图模型因子分解

将概率无向图模型的联合概率表示为图中所有最大团的随机变量函数乘积操作，称为因子分解. 子团节点互相有边连接.而最大团在是找到的任意节点有边连接的最大子图，这意味着其依赖关系被完整考虑. 因为是无方向依赖关系，其函数其实是对节点的连接边的无向（联合）操作.

设\(C\)为无向图\(G\)上的最大团, \(Y_C\)表示其对应随机变量. 则无向图模型\(G\)的联合概率分布\(P(Y)\)可表示为所有最大团势函数乘积。

\[ P(Y) = \frac{1}{Z} \prod_C \Psi (Y_C) \]
\(Z\)是规范化因子。
\[ Z = \sum_Y \prod_C \Psi (Y_C) \]
\( \Psi \) 必须是严格正(因不可能存在负概率)，通常用指数函数\( \exp \)。

参考资料:
[1] 李航; 统计机器学习
[2] Luis Enrique Sucar; Probabilistic Graphical Models Principles and Applications
[3] Daphne Koller,Nir Friedman;Probabilistic Graphical Models Principles and Techniques