2. 条件随机场

给定变量\( X \)时无向图\( Y \)的随机场。

\[ P(Y_v|X, Y_w \neq Y_v) \]

\( Y_W \) 是所有与\( Y_v \)有连接的节点(考虑局部独立性，这里使得条件随机场的\( P(Y|X) \)可描述为\( Y_v \)的联合概率)。

2.1 线性链条件随机场

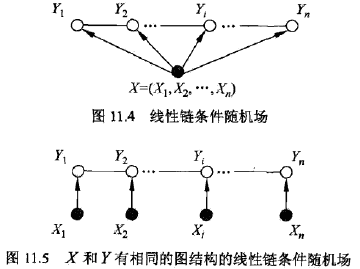
考虑线性链条件随机场，\( X \)表示输入序列，\( Y \)表示输出序列, \( Y_i \)节点只有前后两个连接，按之前条件随机场定义，此时模型简化为：

\[ P(Y | X) = \prod_{i=1}^n P(Y_i | X, Y_{i-1}, Y_{i+1}) \]

设\( Y_0, Y_{n+1} \)为起始之前的节点和结束之后的节点。

2.1.1 势函数

在线性链条件随机场中。每个最大团只由相邻两个节点组成。\( (Y_{i-1},Y_i) \); \( ( Y_i, X_i ) \)。势函数实际上只有两种类型。且这里考虑到函数是\( \exp \)，求积等于指数求和，因此，用势函数定义的线性链条件概率场模型如下：

\[\begin{align}
p(y|x) &=\frac{1}{Z(x)} \exp \left[ \sum_{i,k} \lambda_k t_k(y_{i-1}, y_i) + \sum_{i,l} \mu_l s_l(y_i, x_i) \right] \\
Z(x) &= \sum_y \exp \left[ \sum_{i,k} \lambda_k t_k(y_{i-1}, y_i) + \sum_{i,l} \mu_l s_l(y_i, x_i) \right]
\end{align} \]

其中,\( i=1,2,3, \cdots, n+1 \), \( t_k, s_l \)分别是对应其特征函数(值域：{0,1})，\( \lambda,\mu \)是对应特征权重，很显然这是对数线性模型(最大墒模型-特征函数)。

2.2 模型描述

上面的公式可看出，特征函数在每个\(y_i, x_i\)时有多次定义,且对应各自不同的权重参数。据此可将模型简化描述。

2.2.1 内积形式

考虑合并\(t_k, s_l, \lambda_k, \mu_l\)为带分支单函数和权重。 特征函数和参数数量为\(K=K_1+K_2\)。

\[ f_k(y_{i-1}, y_i, x_i)=
\begin{cases}
t_k(y_{i-1},y_i), & k=1,2,\cdots,K_1 \\
s_l(y_i,x_i), & k=K_1 + l, l=1,2,\cdots,K_2 \\
\end{cases} \\
w_k=
\begin{cases}
\lambda_k, & k=1,2,\cdots,K_1 \\
\mu_l, & k=K_1 + l, l=1,2,\cdots,K_2 \\
\end{cases} \]

于是可将模型改写为:

\[\begin{align}
p(y|x) &=\frac{1}{Z} \exp \sum_{i,k} w_k f_k(y_{i-1}, y_i, x_i) \\
&= \frac{1}{Z} \exp \sum_k w_k \sum_i f_k(y_{i-1}, y_i, x_i)
\end{align} \]

定义：
\[\begin{align}
f_k(y,x) &= \sum_i f_k(y_{i-1}, y_i, x_i) \\
F(y,x) &= [f_1(y,x),f_2(y,x),\cdots,f_k(y,x)]^T \\
w &= [w_1,w_2,\cdots, w_k]^T
\end{align} \]

模型可重写为内积形式：

\[\begin{align}
p_w(y|x) &=\frac{1}{Z_w(x)} \exp( w \cdot F(y,x) ) \\
Z_w(x) &= \sum_y \exp( w \cdot F(y,x) )
\end{align} \]

2.2.2 矩阵形式

设\( M_i(y_{i-1}, y_i, x) \)为相邻两个团的势函数，将所有\( y_{i-1},y_i,x_i \)的势函数写为多个矩阵形式。\(y_{i-1}\)作为行, \(y_i\)作为列。矩阵数量为\(n+i\)，第一个矩阵时\(y_{i-1} \equiv start\),因此只有一行有值，其余都是0。最后一个矩阵时\(y_i \equiv stop \)，因此只有一列有值，其余都是0。

\[\begin{align}
M_i(x) &= \left[M_i(y_{i-1}, y_i, x)\right] \\
M_i(y_{i-1}, y_i, x) &= \exp \sum_k w_k f_k(y_{i-1}, y_i, x_i)
\end{align} \]

例：设\(y \in {a,b,c}\)，则上公式生成的多个矩阵如下：

\[ \begin{align}
M_1(x) &=
\begin{bmatrix}
M_1(start, a, x) & M_1(start, b, x) & M_1(start, c, x) \\
0 & 0 & 0 \\
0 & 0 & 0
\end{bmatrix} \\
M_2(x) &=
\begin{bmatrix}
M_2(a, a, x) & M_2(a, b, x) & M_2(a, c, x) \\
M_2(b, a, x) & M_2(b, b, x) & M_2(b, c, x) \\
M_2(c, a, x) & M_2(c, b, x) & M_2(c, c, x)
\end{bmatrix} \\
\vdots \\
M_{n+1}(x) &=
\begin{bmatrix}
M_{n+1}(a, stop, x) & 0 & 0 \\
M_{n+1}(b, stop, x) & 0 & 0 \\
M_{n+1}(c, stop, x) & 0 & 0
\end{bmatrix} \\
\end{align} \]

输出序列对应的矩阵元素乘积 \( \prod_i^{n+1} M_i( y_{i-1} , y_i, x) \) 刚好对应非规范化概率。而规范化因子就是所有\( M_i(x) \)矩阵的乘积。

\[ Z_w(x) = {M_1(x) M_2(x) \cdots M_{n+1}(x)}_{start, stop} \]

于是任意输出序列\( y \)的条件概率可表示为：

\[ p_w(y|x) = \frac{1}{Z_w(x)} \prod_i^{n+1} M_i(y_{i-1}, y_i, x) \]

参考资料:
[1] 李航; 统计机器学习
[2] Luis Enrique Sucar; Probabilistic Graphical Models Principles and Applications
[3] Daphne Koller,Nir Friedman;Probabilistic Graphical Models Principles and Techniques